

Лабораторная работа №3
Математическое моделирование и автоматизация спектрального анализа сигналов
Цель работы: Освоение методов построения аналитических моделей спектров сигналов.
1. Описать заданный сигнал в виде кусочно-определенной функции f(x) в общем виде (использовать функцию piecewise пакета Maple).
2. Задать численные параметры сигнала на интервале от 0 до 2*Pi.
3. Построить график полученной функции, убедиться в правильности описания сигнала.
4. Выполнить интегральное преобразование Фурье функции f(x)
> 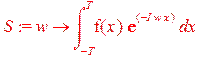
и получить аналитическую зависимость S(w) для спектральной плотности сигнала. Выполнить преобразование Фурье входного сигнала воспользовавшись пакетом интегральных преобразований СКМ Maple. Сравнить результаты.
5. Построить графики полученных в п.4 зависимостей. Пояснить полученные результаты.
6. Получить аналитические зависимости действительной и мнимой частей, амплитудно-частотной и фазо-частотной характеристик спектральной плотности, а также для коэффициентов разложения в ряд Фурье.
7. Распечатать первые 5 коэффициентов разложения в ряд Фурье. Построить графики полученных в п.6 зависимостей. Пояснить полученные результаты.
8. Для самостоятельной проработки (факультативно). Преобразовать исходный сигнал в чётную функцию и выполнить пп. 1- 7 для чётной функции.
9. Выполнить преобразование Лапласа входного сигнала. Выполнить замену оператора pнаj∙w. Сравнить с выражением спектральной плотности, полученным в п.3.
10.Восстановить исходный сигнал из разложения в ряд Фурье, самостоятельно задавшись числом гармоник. Изменяя число гармоник, проследить за точностью восстановления сигнала.
11.Для самостоятельной проработки (факультативно), выполнить задание п.10 в режиме анимации.
12.Сделать выводы по работе.
13.Сохранить протокол работы на диске.
14. Подготовить и распечатать отчет по работе.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.