Исследование математической модели диодного ограничителя с графической вольт-амперной характеристикой

Лабораторная работа №9

Математическое моделирование технических систем с нелинейными характеристиками.

Цель работы: Овладеть навыками построения моделей нелинейного регрессионного анализа и моделирования на технических систем с нелинейными характеристиками.

Часть I.  Исследование математической модели диодного ограничителя с графической вольт-амперной характеристикой

Постановка задачи

1.  Вольтамперную характеристику диода, для которой получена аналитическая аппроксимирующая кривая вида 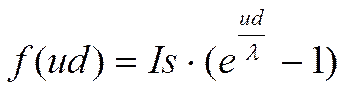, где f(ud) – ток через диод, ud – напряжение на диоде,  использовать согласно варианта из лабораторной работы №4.

2.  Задать математическую модель в виде дифференциального уравнения или системы алгебро-дифференциальных уравнений и выполнить моделирование схемы при ступенчатом и гармоническом внешнем сигнале e(t).

3.  Для самостоятельной проработки: Исследовать влияние значений резистора и ёмкости на вид функции напряжения на емкости.

4.  Для самостоятельной проработки: Получить спектр выходного сигнала при гармоническом входном сигнале. Сделать выводы.

Исходные данные для выполнения лабораторной работы

Исходными данными для работы являются:

Экспериментальная кривая вольт-амперной характеристики диода в соответствии с вариантом задания ЛР№4.

e(t) – функция ЕДС – ступенчатая и гармоническая синусоидальная;

R –  сопротивление;

C –емкость;

U₀ – начальное значение напряжения;

Т – время исследования.

Таблица 1.1 - Таблица исходных данных

Для варианта	C	R	U0	T мкс	e0 (В)
Нечетные варианты	10-5	20	0	200	1
Четные варианты	1,12∙10-5	19	0	210	1,1

Описание математической модели

Электрическая цепь, приведенная на рисунке 1.1, описывается дифференциальным уравнением вида, где u(t) – напряжение на конденсаторе:

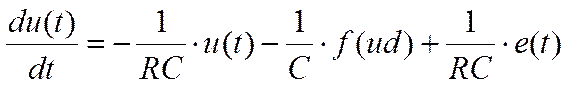
Входной сигнал e(t) в будем определять :

1. По формуле:

 

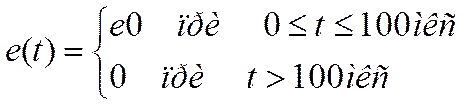
2. В виде гармонического синусоидального сигнала (параметры задать самостоятельно).

Схема цепи:

Часть2. Исследование математической модели электрической  цепи с туннельным диодом

Постановка задачи

1.  Вольтамперную характеристику диода, для которой получена аналитическая аппроксимирующая кривая вид,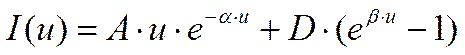

где I(u) – ток через диод, u – напряжение на диоде, использовать согласно варианта из лабораторной работы №4.

2.  Задать математическую модель в виде системы алгебро-дифференциальных уравнений и выполнить моделирование схемы при постоянном и гармоническом внешнем сигнале e(t).

3.  Для самостоятельной проработки: Исследовать влияние значений резистора, индуктивности, ёмкости и входного постоянного сигнала на вид функции напряжения на емкости. Определить пределы параметров, при которых при постоянном внешнем сигнале колебательный процесс в схеме не наблюдается.

4.  Для самостоятельной проработки: Получить спектр выходного сигнала. Сделать выводы.

Исходными данными для лабораторной работы являются:

Е – ЕДС – для всех вариантов принять равным 0.3В.

R –  сопротивление;

C –емкость;

L –индуктивность;

u₀ – начальное значение напряжения;

i₀ – начальное значение тока;

Т – время исследования.

Таблица 2.1- Таблица исходных данных

Для варианта	C Ф	R Ом	L Гн	T с
Чётные варианты	10-11	10	10-7	4∙10-6
Нечетные варианты	0.88∙10-11	7	95∙10-9	3.8∙10-6

Описание математической модели

Электрическая цепь, приведенная на рисунке 2.1, описывается системой дифференциальных уравнений вида:

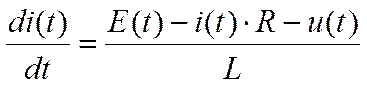
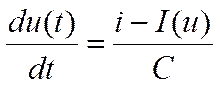
Функция для аппроксимации вольт-амперной  характеристики  диода имеет вид:

При решении системы дифференциальных уравнений принять i₀ и u₀ (начальные значения тока и напряжения) равными 0.

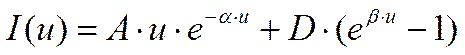
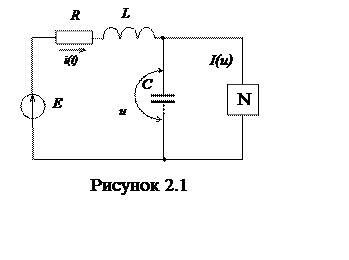Схема цепи: