Изучение базовых конструкций языка VHDL. Моделирование передаточных функций

Аврамов Р.А. ЭМ-51

Лабораторная работа №2

Изучение базовых конструкций языка VHDL. Моделирование передаточных функций.

Цель работы: изучение базовых конструкций языка VHDL. Моделирование передаточных функций.

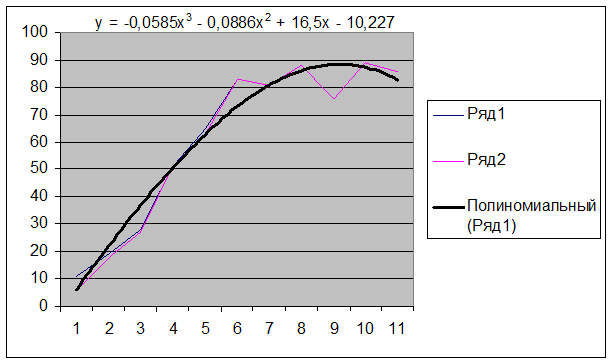
Рисунок 1 – График, аппроксимация и уравнение, полученные в Excel

--------------------------------------------------------------------------------------------

Исходный VHDL-текст программы

--------------------------------------------------------------------------------------------

library IEEE;

use IEEE.STD_LOGIC_1164.all;

use ieee.std_logic_arith.all;

entity pol is

             port(

                         in1 : in std_logic_vector (7 downto 0);

                         out1 : out std_logic_vector (15 downto 0)

                 );

end pol;

architecture pol of pol is

begin

            process (

            in1 )

            variable x : INTEGER;

            variable y : INTEGER;

            variable sum : real;

            variable cur : real;

            begin

                        x := conv_integer (unsigned (in1) );

                        cur := real (x);

                        sum := (cur**3) * (-0.0585) + (cur**2) * (-0.0886) + (cur) * (16.5) -10.227;

                        y := integer (sum);

                        out1 <= std_logic_vector (conv_unsigned (y, 16));

            end process;  

end pol;

--------------------------------------------------------------------------------------------

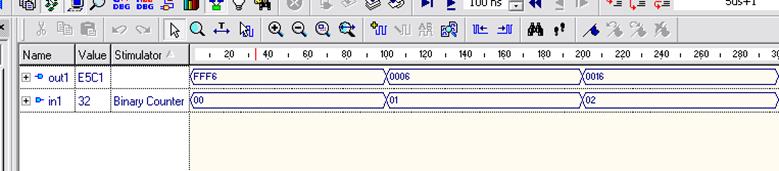
Рисунок 2 – Скриншот Waveform

-------------------------------------------------------------------------------------------------------------

Сравнение значений, полученных с помощью Active HDL

11	11
19	18
28	27
51	51
65	63
83	83
81	81
88	88
76	76
89	89
86	86

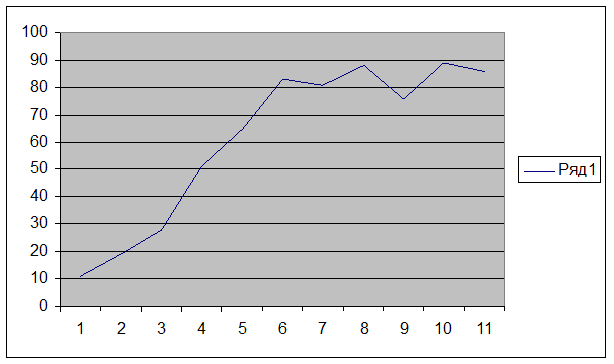
Рисунок 3 – График, построенный по значениям из Active HDL

--------------------------------------------------------------------------------------------

Исходный VHDL-текст синтезируемой программы

--------------------------------------------------------------------------------------------

library IEEE;

use IEEE.STD_LOGIC_1164.all;

use ieee.std_logic_arith.all;

entity pol is

             port(

                         in1 : in std_logic_vector (15 downto 0);

                         out1 : out std_logic_vector (31 downto 0)

                 );

end pol;

architecture pol of pol is

begin

            process (

            in1 )

            variable x : INTEGER;

            variable y : INTEGER;

            begin

                        x := conv_integer (unsigned (in1) );

            y := (x*x*x)*(-2)/(32*32*32) + (x*x)*(-3)/(32*32) + x*(528)/32 - 327;

            --         y := integer (sum);

                        out1 <= std_logic_vector (conv_unsigned (y, 32));

            end process;  

end pol;

--------------------------------------------------------------------------------------------

Рисунок 3 – Waveform для синтезируемой программы

--------------------------------------------------------------------------------------------

196	6,125
701	21,90625
1176	36,75
1609	50,28125
1988	62,125
2301	71,90625
2536	79,25
2681	83,78125
2724	85,125
2653	82,90625
2456	76,75

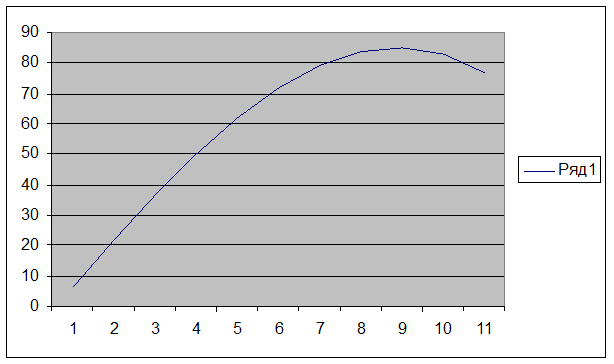
Рисунок 4 – График значений аппроксимирующей функции для синтезируемой программы

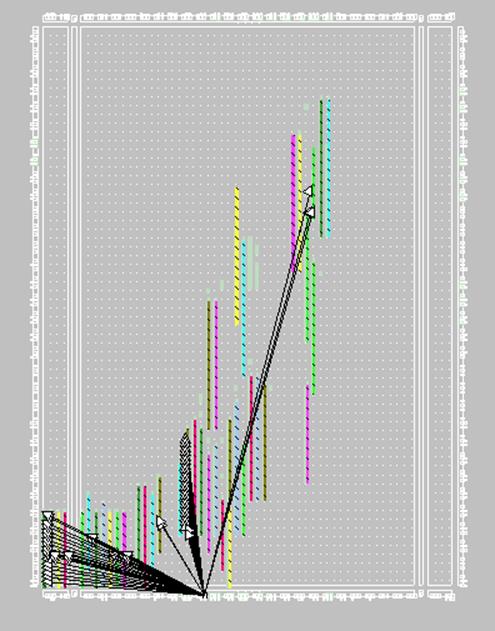
Рисунок 5 – Размещение на кристалле

Вывод:

1)  в работе в Excel реализована полиномиальная аппроксимация функциональной зависимости, найдено уравнение, описывающее данную зависимость;

2)  в Active HDL описан заданный процесс, получен Waveform и по значениям построен график аппроксимирующей функции;

3)  создана синтезируемая реализация аппроксимирующей функции и размещением её на кристалле.

Значения исходной функциональной зависимости и аппроксимирующей функции, полученные разными способами, практически совпадают. При размещении на кристалле программа заняла значительный объём (выбран был кристалл Spartan3).