Ошибка типа 0 ® 1 на входе элемента ИЛИ исправляется на выходе элемента И третьего каскада. Число элементов И первого каскада схемы возросло до четырех, число независимых копий входного сигнала — до восьми Дальнейший рост числа каскадов схемы вызывает увеличение числа элементов в каждом предыдущем каскаде и числа независимых входных сигналов. Однако все ошибки могут быть исправлены схемами с четырьмя одинаковыми элементами в каждом каскаде благодаря специальному соединению между собой входов элементов одного каскада. Схема (рисунок 12, б) обладает теми же свойствами по исправлению ошибок, что и схема, приведенная на рисунке 12, а. На этой схеме объединены входы элементов первого каскада. В результате вместо восьми потребовалось четыре независимых входных сигнала.
Объединение входов элементов каскада приводит к появлению на выходах каскада двойной ошибки, обусловленной одиночной ошибкой.
Например, ошибка 1 ® 0 на входе х(1) (см. рисунок 12, б) вызывает такую же ошибку на выходах элементов 1 и 3 первого каскада схемы. Однако обе эти ошибки исправляются следующим каскадом схемы, так как поступают на входы различных его элементов. Очевидно, что если бы обе ошибки поступили на вход одного элемента ИЛИ второго каскада, это вызвало бы появление ошибки на его выходе, а, следовательно, и на выходе всей схемы.
Рассмотрим
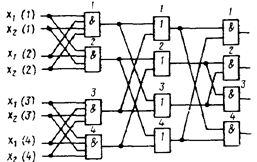
трехкаскадную схему с учетверенными связями (рисунок 13).
Рисунок 13 — Схема И-ИЛИ-НЕ с учетверенными связями
Элементы И первого каскада имеют по два сдвоенных входа, т.е. помимо задачи исправления ошибок, они в данном случае выполняют и свою основную задачу реализацию логических функции. Аналогично могут быть включены элементы и других каскадов (соответствующие их входы не показаны для упрощения рисунка). Входы элементов каждого каскада объединены в соответствии с определенной формулой. Для первого каскада имеет место формула [1, 2 — 3, 4] (объединены входы первого и второго, а также третьего и четвертого элементов), для второго каскада формула [1, 3 — 2, 4] и для третьего каскада формула [1, 4 — 2, 3].
Необходимым условием исправления ошибок является объединение входов элементов двух соседних каскадов схемы в соответствии с различными формулами. Это обеспечивает невозможность попадания двух ошибок, возникающих на выходе какого-либо каскада в результате одиночной ошибки предыдущего каскада, на входы одного и того же элемента последующего каскада. В этом случае (как было показано на примере схемы рисунок 12, б) двойные ошибки исправляются. Если в соответствии с логической структурой схемы необходимо соединить последовательно несколько каскадов из одинаковых элементов, их включают по одной и той же формуле. В этом случае ошибки обоих каскадов исправляются первым последующим каскадом из элементов другого типа.
Вернемся к схеме, приведенной на рисунке 11, в. Включим на выходе элементов И первого каскада инверторы (см. рисунок 11, г). Инвертор меняет на противоположный тип ошибки, имеющейся на его входе. Поэтому в данной схеме для исправления ошибок на входах элементов первого каскада после инверторов вместо элемента ИЛИ следует установить элемент И. Из этого следует, что схемы (см. рисунок 11, д), представляющие собой последовательное включение каскадов из элементов И-НЕ (или ИЛИ-НЕ) обладают способностью исправлять одиночные ошибки обоих типов.
Избыточную комбинационную схему с учетверенными связями (рисунок 14) строят по структуре неизбыточной схемы заменой каждого ее элемента каскадом из четырех соответствующих элементов со сдвоенными входами.
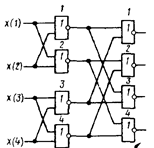
Рисунок 14 — Схема из двух каскадов элементов ИЛИ-НЕ с учетверенными связями
Необходимо правильно чередовать
формулы объединения входов элементов различных каскадов. Элементы двух
последних каскадов схемы должны исправлять ошибки обоих типов. На рисунке 15
показан пример построения схемы, реализующей функцию 
.
В ней для каждого элемента с учетверенными связями указана формула объединения
входов.
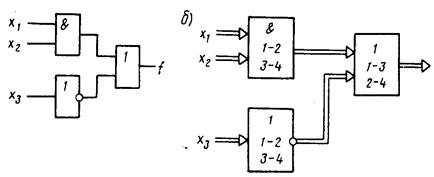
Рисунок 15 — Неизбыточный (а) и избыточный (б) варианты избыточной схемы с учетверенными связями
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.