Автоматизация математических расчетов в системе компьютерной математики Maple (Лабораторная работа № 1)

Лабораторная работа №1

«Автоматизация математических расчетов в системе компьютерной математики Maple»

Цель работы: Освоение  аналитических вычислений и процесса  их автоматизации в СКМ Maple.

Задание к лабораторной работе:

1.   Войти в операционную систему и загрузить пакет Maple.

2.   Вызвать функции sqrt(3); sqrt(3.); sqrt(3.): 3*sin(1); 3*sin(1.);

Сравнить результаты вычислений.

Вызвать функции evalf(sqrt(3)); evalf(sin(1)); получить и сравнить результаты.

3. Для функции sqrt(3)  выполнить перевод входного и выходного форматов из текстовой нотации в математическую и наоборот. Перевести строку вызова функции в формат текстового комментария и наоборот.
4. Освоить операции раздела Insert (создание секции, группы,  параграфа,  включение текстового комментария в секцию и группу).

4.1.Выполнить установку режимов ввода текста и ввода выражений.

4.2.Выполнить вставку текстовой области (Paragraph).

4.3.Выполнить вставку вычислительной группы.

4.4.Выполнить вставку кнопки секции (Section).

4.5.Выполнить вставку кнопки подсекции (Subsection), создать Параграф и Группу в подсекции, снабдить Секцию и Подсекцию комментарием.

Далее перед каждым следующим пунктом работы делать текстовый комментарий к выполняемому пункту. Например, «Решить аналитически алгебраическое уравнение относительно переменной X».

5. Решить аналитически алгебраическое уравнение A*x^2 + B*x + C = D относительно переменных  x и B.  

Решить уравнения относительно переменной х:

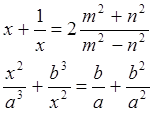
Использовать функцию solve(f(x),x).

6.  Разложить функцию в степенной ряд и ряд Тэйлора ( series(); taylor(); ). Индивидуальное задание взять из таблицы №2.

7. Преобразовать выражение sinh(x) + cos(x)  в экспоненциальную форму,  используя функцию (convert();).
8. Преобразовать и упростить выражение

с помощью функции  simplify();

9.  Выполнить эквивалентные преобразования (expand();):  

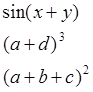
Разложить  выражения на множители (factor()):

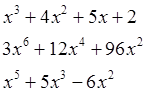
 Убедиться в эквивалентности преобразований.

10. Вычислить производную функции (diff;). (индивидуальное задание взять из таблицы №5). Получить численные значения результирующей функции в двух точках: х1 и х2.

11. Вычислить неопределенный интеграл функции (int;). Вычислить определенный интеграл функции (int;). Получить численное значение. (индивидуальное задание взять из таблицы №6).

12. Используя пакет расширения inttrans, выполнить и убедиться в эквивалентности преобразований (индивидуальное задание взять из таблицы №2):

12.1 Прямое ( laplace(); ) и обратное ( invlaplace(); ) преобразование Лапласа;

12.2 Прямое ( fourier(); ) и обратное ( invfourier(); ) преобразование Фурье

13. Решить ОДУ (dsolve;). (индивидуальное задание взять из таблицы №7).

14. Построить график функции (plot; plot3d;). (индивидуальное задание взять из таблиц №3 и 4).

15. Оформить выводы по работе.

16. Сохранить протокол работы на диске.

17. Подготовить и распечатать отчет по работе.