


Лабораторная работа №3
«Автоматизация аналитических вычислений в системе компьютерной математики MatLab»
Цель работы: Освоение аналитических вычислений и решения дифференциальных уравнений и систем, а также процесса их автоматизации в СКМ MatLab.
Выполнил Громов Евгений, ЭМ-22, вариант 10.
Задание к лабораторной работе:
1. Разложить функцию в ряд Тэйлора.
Листинг программы:
taylor(exp(-x)*sin(x))
Результат расчёта:
ans =
x-x^2+1/3*x^3-1/30*x^5
2. Преобразовать и упростить выражение
![]()
с помощью функции simplify();
Листинг программы:
syms x
simplify(cos(x)^5+sin(x)^4+2*cos(x)^2-2*sin(x)^2-cos(2*x))
Результат расчёта:
ans =
cos(x)^5+cos(x)^4
3. Выполнить эквивалентные преобразования:
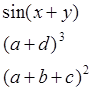
Листинг программы:
syms x y a b c d
expand([sin(x+y) (a+d)^3 (a+b+c)^2])
Результат расчёта:
ans =
[sin(x)*cos(y)+cos(x)*sin(y), a^3+3*a^2*d+3*a*d^2+d^3, a^2+2*a*b+2*a*c+b^2+2*b*c+c^2]
4. Разложить выражения на множители:
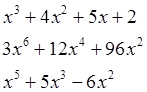
Убедиться в эквивалентности преобразований.
Листинг программы:
syms x
factor(x^3+4*x^2+5*x+2)
expand((x+2)*(x+1)^2)
factor(3*x^6+12*x^4+96*x^2)
expand(3*x^2*(x^4+4*x^2+32))
factor(x^5+5*x^3-6*x^2)
expand(x^2*(x-1)*(x^2+x+6))
Результат расчёта:
ans = (x+2)*(x+1)^2
ans = x^3+4*x^2+5*x+2
ans = 3*x^2*(x^4+4*x^2+32)
ans = 3*x^6+12*x^4+96*x^2
ans = x^2*(x-1)*(x^2+x+6)
ans = x^5+5*x^3-6*x^2
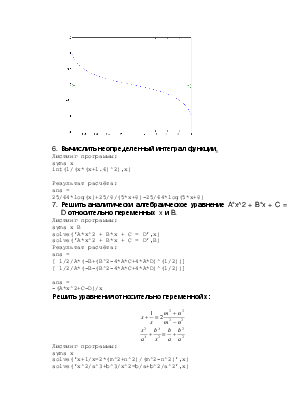
5. Вычислить производную функции. Построить график исходной функции и её первой производной (пределы изменения аргумента выбрать самостоятельно) и получить приближённые численные значения результирующей функции в двух точках: х1 и х2.
Листинг программы:
syms pr
pr=diff('asin(x)/(x^2-2.5)')
x=-1:0.01:1;
fn=asin(x)./(x.^2-2.5);
fnp=diff(fn);
fnp(201)=fnp(200);
plot(x,fn,x,fnp)
x=[1.4; 0.65];
asin(x)./(x.^2-2.5)
Результат расчёта:
pr =
1/(1-x^2)^(1/2)/(x^2-2.5)-2*asin(x)/(x^2-2.5)^2*x
ans =
-2.9089 + 1.6056i
-0.3406
График:
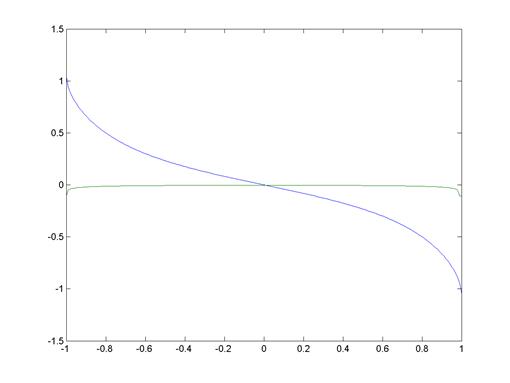
6. Вычислить неопределенный интеграл функции.
Листинг программы:
syms x
int(1/(x*(x+1.6)^2),x)
Результат расчёта:
ans =
25/64*log(x)+25/8/(5*x+8)-25/64*log(5*x+8)
7. Решить аналитически алгебраическое уравнение A*x^2 + B*x + C = D относительно переменных x и B.
Листинг программы:
syms x B
solve('A*x^2 + B*x + C = D',x)
solve('A*x^2 + B*x + C = D',B)
Результат расчёта:
ans =
[ 1/2/A*(-B+(B^2-4*A*C+4*A*D)^(1/2))]
[ 1/2/A*(-B-(B^2-4*A*C+4*A*D)^(1/2))]
ans =
-(A*x^2+C-D)/x
Решить уравнения относительно переменной х:
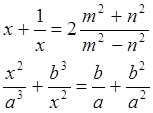
![]()
Листинг программы:
syms x
solve('x+1/x=2*(m^2+n^2)/(m^2-n^2)',x)
solve('x^2/a^3+b^3/x^2=b/a+b^2/a^2',x)
Результат расчёта:
ans =
[ (m+n)/(m-n)]
[ (m-n)/(m+n)]
ans =
[ a^(1/2)*b]
[ -a^(1/2)*b]
[ b^(1/2)*a]
[ -b^(1/2)*a]
Использовать функцию solve(f(x),x).
8. Решить аналитически системы алгебраических уравнений:
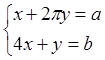
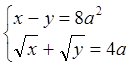
Листинг программы:
syms x y
[x,y]=solve('x+2*Pi*y=a','4*x+y=b')
[x,y]=solve('x-y=8*a^2','sqrt(x)+sqrt(y)=4*a')
Результат расчёта:
x = -(-2*pi*b+a)/(-1+8*pi)
y = (4*a-b)/(-1+8*pi)
x = 9*a^2
y = a^2
9. Решить численно ОДУ первого и второго порядка. Построить графики полученных в результате решения функций.
![]() ,
, ![]() , xn=2, xk=5, n=1000.
, xn=2, xk=5, n=1000.
Листинг программы:
function rez=myfunc(x,y)
rez=(4*x^3+3*x^2-y(1))/x;
y0=1;
[X,Y]=ode23(@myfunc,[2 5],y0,1000)
plot(X,Y)
График:
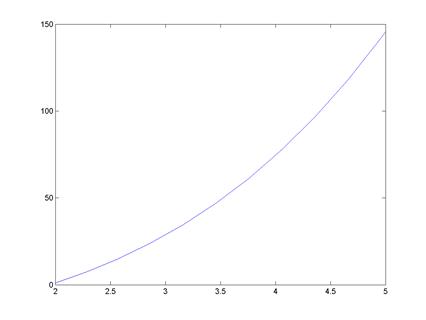
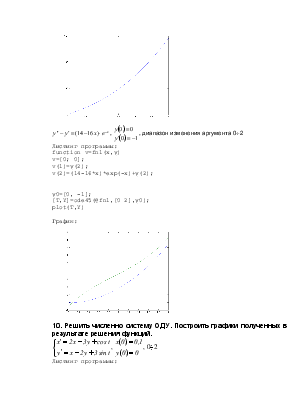
![]() ,
, 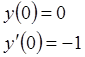 , диапазон
изменения аргумента 0¸2
, диапазон
изменения аргумента 0¸2
Листинг программы:
function v=fn1(x,y)
v=[0; 0];
v(1)=y(2);
v(2)=(14-16*x)*exp(-x)+y(2);
y0=[0, -1];
[T,Y]=ode45(@fn1,[0 2],y0);
plot(T,Y)
График:
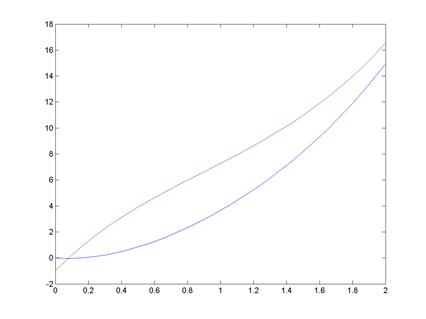
10. Решить численно систему ОДУ. Построить графики полученных в результате решения функций.
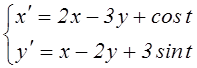 ,
, 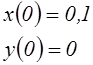 , 0¸2
, 0¸2
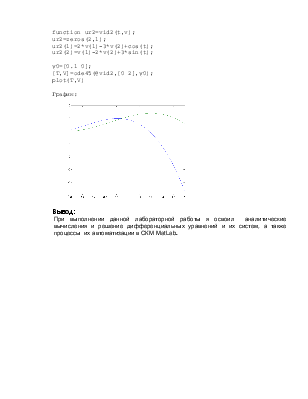
Листинг программы:
function ur2=vid2(t,v);
ur2=zeros(2,1);
ur2(1)=2*v(1)-3*v(2)+cos(t);
ur2(2)=v(1)-2*v(2)+3*sin(t);
y0=[0.1 0];
[T,V]=ode45(@vid2,[0 2],y0);
plot(T,V)
График:
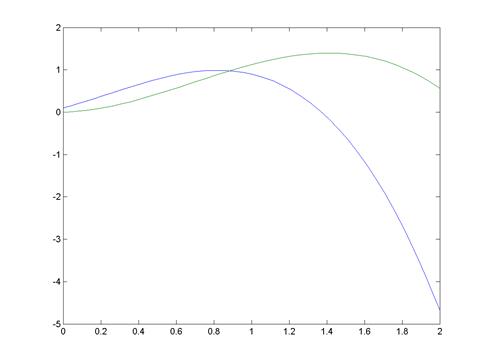
Вывод:
При выполнении данной лабораторной работы я освоил аналитические вычисления и решение дифференциальных уравнений и их систем, а также процессы их автоматизации в СКМ MatLab.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.