Автоматизация аналитических вычислений в системе компьютерной математики MatLab (Лабораторная работа № 3)

Лабораторная работа №3

«Автоматизация аналитических вычислений в системе компьютерной математики MatLab»

Цель работы: Освоение  аналитических вычислений и решения дифференциальных уравнений и систем, а также  процесса  их автоматизации в СКМ MatLab.

Задание к лабораторной работе:

1. Разложить функцию в ряд Тэйлора ( taylor(); ). Индивидуальное задание взять из таблицы №2.

2.  Преобразовать и упростить выражение

с помощью функции simplify();

3.  Выполнить эквивалентные преобразования (expand();):  

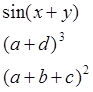
4. Разложить  выражения на множители (factor()):

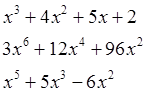
 Убедиться в эквивалентности преобразований.

5.  Вычислить производную функции (diff;). (индивидуальное задание взять из таблицы №5). Построить график исходной функции и её первой производной (пределы изменения аргумента выбрать самостоятельно) и получить приближённые численные значения результирующей функции в двух точках: х1 и х2.

6.  Вычислить неопределенный интеграл функции (int;). (Индивидуальное задание взять из таблицы №6).

7.  Решить аналитически алгебраическое уравнение A*x^2 + B*x + C = D относительно переменных  x и B. 

Решить уравнения относительно переменной х:

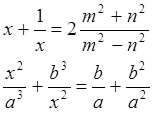
Использовать функцию solve(f(x),x).

8. Решить аналитически системы алгебраических уравнений:

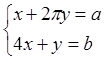
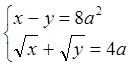
9. Решить численно ОДУ первого и второго порядка. (Индивидуальное задание взять из таблиц №7.1 и 7.3). Построить графики полученных в результате решения функций.

10. Решить численно систему ОДУ. (Индивидуальное задание взять из таблицы №7.2). Построить графики полученных в результате решения функций.

11. Оформить выводы по работе.

12. Сохранить протокол работы на диске.

13. Подготовить и распечатать отчет по работе.

При выполнении пп. 9 и 10 см. Приложение 1.

Приложение 1.

Краткие теоретические сведения и примеры описания функций при численном решении ОДУ и их систем

Например, при решении дифференциального уравнения вида:

функция, описывающая правую часть уравнения, имеет вид:

function ur=vid(x,y);

ur=-y(1)+2*x;

При решении системы дифференциальных уравнений:

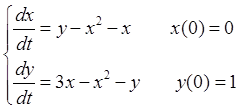
 выполнена замена переменных: v(1)- x, v(2)- y, при этом

функция имеет следующий вид:

functionur2=vid2(t,v);

ur2=zeros(2,1);

ur2(1)=v(2)-v(1)^2-v(1);

ur2(2)=3*v(1)-v(1)^2-v(2);

Стандартные функции решения ОДУ содержат ряд параметров, общий вид вызова функции следующий:

ИМЯФУНКЦИИ (ОДУ, Д, НУ,  О)

Здесь ОДУ – дескриптор функции, описывающей одно дифференциальное уравнение или система дифференциальных уравнений, Д – диапазон, на котором ищется решение ОДУ, НУ -  начальные условия, О-опции – необязательный параметр, задающий дополнительные условия решения.

Например, для ОДУ задания 1 М-файл решения имеет вид:

y0=1;

[X,Y]=ode15s(@vid,[0 3],y0);

plot(X,Y)

Для  системы ОДУ задания 2 М-файл решения имеет вид:

y0=[0 1];

[T,V]=ode45(@vid2,[0 5],y0);

plot(T,V)