Многомерная безусловная минимизация функций, градиентные методы, страница 3

Необходимое условие точки минимума не выполняется, продолжаем процесс поиска точки минимума до достижения заданной точности.

Результат работы программы:           

X1 = 4.99922 X2 = 5.99816 y(x1,x2) = -86 Result was found in 118 iterations

Вывод: В ходе лабораторной работы была разработана программа для многомерной безусловной минимизации функции градиентным методом с дробленим шага. Реализованный метод оказался не очень эффекимвным. Это произошло из-за того что функция имеет очень крутые склоны, и начальное приближение было выбранно так, что промежуточные ответы прыгали из стороны в сторону от решения. При более удачном выборе начального приближения, поиск решения мог бы занять всего пару итераций (при чем это не значит что его нужно выбирать ближе к ответу – предугадать каное из начальних приближений более эффективно для данного метода очень сложно ведь зависит от производных функции).

Расчетно-графическая работа

Метод Эйлера

Функция:

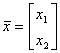, n=2;

         Используя необходимое условие точки минимума формируем систему:

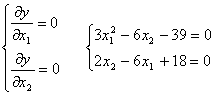
         Решаем систему находим стационарные точки:

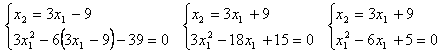
Теперь  надо выбрать точки минимума. Используем достаточное условие точки минимума: в каждой из точек вычисляем матрицу Гесса и проверяем ее положительную определенность по критерию Сильвестра.

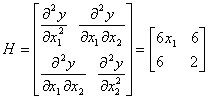
, => - седловая точка

, => - точка минимума.