Proposal of Implementing a 64-bit RSA on FPGA
Qian Wan, Jing Lu
Motivation:
Nowadays, more and more reconfigurable hardware components are used on the Internet due to its low cost, high performance and reconfigurability. Such components need secure channels for remote control and reconfiguration. The RSA public key cryptographic algorithm can be used in these applications as a method of exchanging secret information such as keys. RSA algorithm is a secure, high quality, public key algorithm. However, it is very computationally intensive, operating on very large (typically thousands of bits long) integers. We have seen mostly software implementations of RSA algorithm. Although commercial Application specific standard products (ASSPs) like the security processors offered by several vendors have a much higher RSA performance than software implementation, they are inflexible and expensive. With the exponential increases in FPGA size over time (Moore’s law), it is possible to implement a relatively high performance, user parameterizable and synthesizable RSA at low cost on FPGA.
Due to the computation complexity and limited time of this class project, we intend to implement a 64-bit RSA on FPX platform with a XIlinx Vertex 2000E FPGA on it. We will try to design each module to be extensible and configurable, so that our work can be easily extended to implement an RSA with more bits. Due to the resource limitation on the FPGA chip, we decide not to use pipelined architecture. Instead, we will use iterative architecture for fast computations, so that we can reuse modules without decreasing the overall throughput.
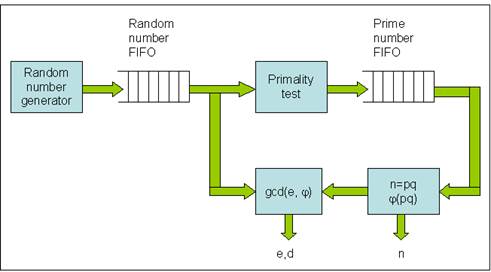
Description:
* Random number Generator:
Use LFSR (Linear Feedback Shift Register) to generate 64-bit pseudo random numbers in sequence.
* Random number FIFO:
A fixed size register file storing random numbers in a FIFO fashion. If FIFO is full, Random number generator will stall. This will save power.
* Primality test:
Take out a random number from Random number FIFO and test if it is a prime. If not, take another random number and test again until it find one. Then put the prime into a downstream Prime number FIFO.
* Prime number FIFO:
A fixed size register file storing prime numbers in a FIFO fashion. If FIFO is full, Primality test will stall. This will save power. Stored primes can be used immediately for generating new public/private key pair when needed.
* n=pq, j(pq):
Take out two primes as p and q. Compute n and j.
* gcd(e, j):
Take out a random number from Random number FIFO and compute e and d using extended Euclid’s algorithm.
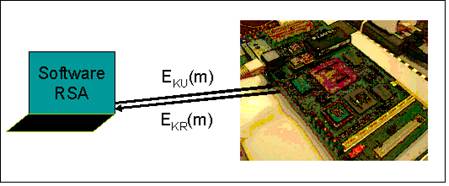
In the testing setup, a PC with RSA software is directly connected to the FPX. First, the PC requests public key (KU) from the FPX. After obtaining KU, it encrypt a message m using KU and sends EKU(m) back. The FPX will decrypt EKU(m) and send EKR(EKU(m)) back to the PC. PC will compare EKR(EKU(m)) with m to determine if the RSA on the FPX generates the right key pair.
The most difficult part is the implementation of the modular arithmetic operations. We intend to use Montgomery’s method for modular multiplication. Design scalability is also very challenging.
Jing Lu (jl1@arl.wustl.edu) is responsible for most hardware implementation
Qian Wan (qw2@arl.wustl.edu) is responsible for testing related hardware and software components, and testing setup.
Week1: Design modular addition module and random number generator.
Week2: Design modular multiplication module and FIFOs.
Week3: Simulating and debugging each moduls.
Week4: Construct and test system.
Week5: writing report.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.