Основные понятия и определения ИИТ. Теория измерений. Средства электрических измерений

Совокупные измерения: неоднократные измерения одноименных величин. Искомые значения величин находят решением системы уравнений, составленных из результатов прямых измерений различных сочетаний этих величин.

Например, определение взаимоиндуктивности между катушкамиL₁, L₂ путём двукратного измерения их общей индуктивности. Сначала катушки соединяют так, чтобы их магнитные поля складывались. Тогда общая индуктивность

L₀₁ = L₁ + L₂ + 2M₁₂,

гдеM₁₂ – взаимоиндуктивность. Затем катушки соединяют так, чтобы их магнитные поля вычитались и измеряют общую индуктивность      

L₀₂ = L₁ + L₂ - 2M₁₂.

Значение M₁₂ определяется с помощью решения уравнения: M₁₂ = (L₀₁ - L₀₂)/4.

Этот вид измерений используется в силу технических условий (нельзя разобрать схему или применить другой вид измерений).

Методы прямых измерений

Метод непосредственной оценки: значение измеряемой величины определяют непосредственно по отсчетному устройству измерительного прибора.

Данный метод дает значение измеряемой величины непосредственно, без каких - либо дополнительных действий со стороны лица, проводящего измерение. Этому методу свойственна быстрота процесса измерения, что делает его часто незаменимым для практического использования, хотя точность измерения обычно бывает ограниченной.

Методы сравнения с мерой: одновременное или разновременное сравнение двух однородных независимых друг от друга величин – измеряемой и известной.

В зависимости от требований и технических возможностей используют:

-  метод дополнения: измеряемую величину дополняют мерой и получают заданное суммарное значение;

-  дифференциальный метод: на измерительный прибор воздействует разность из меряемой величины и меры (рис. 1.4).

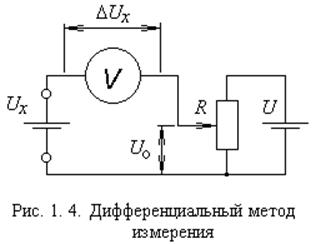Чем меньше данная разность, тем меньше погрешность, вносимая прибором. Это объясняется тем, что точность меры обычно намного выше точности измерительного прибора. Например, необходимо измерить напряжение 100 В измерительным прибором, у которого        δ =1%, погрешностью меры пренебрегаем. При использовании метода непосредственной оценки,  согласно (1.4)  D₁=1 В. Пусть мера формирует напряжение U₀=90 В (дифференциальный метод). Тогда на измерительный прибор подается напряжение DU_X =10 В, следовательно, D₂ = 0,1 В и погрешность измерения уменьшилась в 10 раз. Этот метод применяется, например, в неуравновешенном измерительном мосте;

-  нулевой метод: разность измеряемой величины и меры доводится до нуля регулированием значения меры. Показания снимаются по шкале меры.

Это частный случай дифференциального метода. Он более точен, чем предыдущий, так как важна не точность, а чувствительность измерительного прибора, который служит индикатором равенства меры и измеряемой ФВ. Метод используется, например, в уравновешенном измерительном мосте. Можно применять меры, во много раз меньшие измеряемой величины (неравноплечие весы). По сравнению с дифференциальным методом, недостаток нулевого заключается в необходимости иметь меры, воспроизводящее любое значение известной величины без существенного понижения точности;

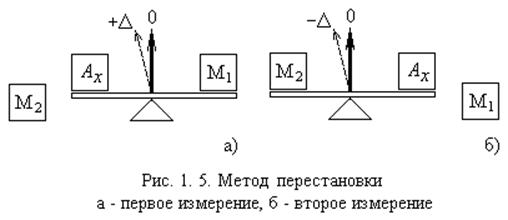
-  метод перестановки: измеряемую и известную величины сравнивают (рис. 1.5) до и после их взаимной перестановки.

Например, добиваются совпадения стрелки весов с нулевой отметкой в обоих случаях. Результат определяется как среднее значение известной величины. Исключается систематическая погрешность D, которая возникает из-за возможного отклонения стрелки весов от нулевой отметки до проведения измерений:

                      A_X = M₁ = M + D, при A_изм.1 =0; A_X = M₂ = M - D, при A_изм.2 =0,

результат:                                       A_X = (M₁ + M₂)/2 = M;

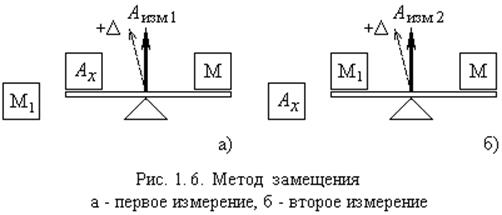Если величины мер регулируются дискретно с шагом DМ, то общая