Исследование переходных процессов в схемах с распределёнными параметрами

Министерство образования и науки РФ

Федеральное Агентство по Образованию

Государственное Образовательное Учреждение

Высшего Профессионального Образования

Новосибирский Государственный Технический Университет

Кафедра ТЭВН

Лабораторная работа №3

ИССЛЕДОВАНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ В СХЕМАХ С РАСПРЕДЕЛЁННЫМИ ПАРАМЕТРАМИ

 

      Факультет: энергетики

      Группа: ЭН1-82

      Студент: Присекин А.И.          

      Преподаватель: Цуркан  Н.В.

      Дата:

Новосибирск 2011

Цель работы: ознакомиться с методикой исследования переходных процессов в схемах с распределёнными параметрами. Для заданного варианта схемы разработать математическую модель, реализовать её на ПЭВМ, рассчитать переходный процесс и провести анализ полученных результатов.

Исходные данные

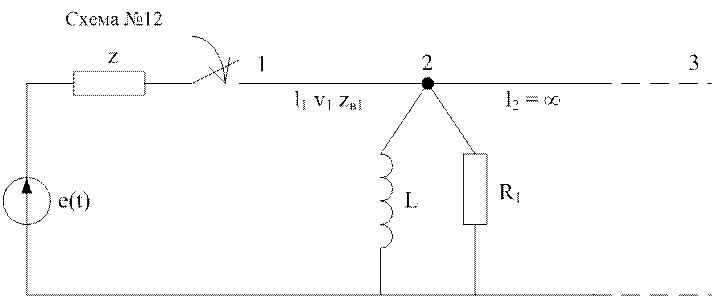
z = 40 Ом; Z_в1 = 40 Ом; Z_в2 = 40 Ом; R₁ = 80 Ом; l₁ = 1800 м; l₂ = ∞; v₁ = 150 м/мкс; v₂ = 300 м/мкс; L = 0,1 мГн.

      Линию бесконечной длины (l₂) заменим активным сопротивлением, равным волновому и полученное сопротивление сложим параллельно с сопротивлением R₁. Это будет сопротивление R₂. В итоге схема примет следующий вид:

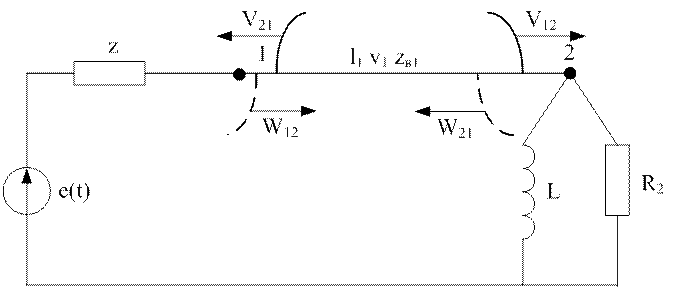
Математическая модель:

Уравнения узла 1

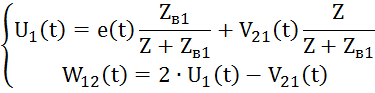
Уравнения узла 2

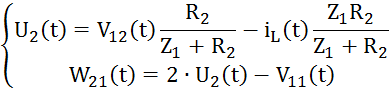
Ток i_L(t) в уравнении узла 2 определяется путём решения дифференциального уравнения  неявным методом трапеций.

Решение уравнения на (к + 1)-м шаге интегрирования можно представить с использованием формулы Ньютона-Лейбница

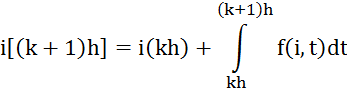
Вычисление интеграла с помощью метода трапеций даёт следующий результат:

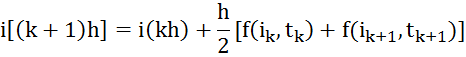
В нашем случае:

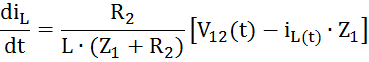
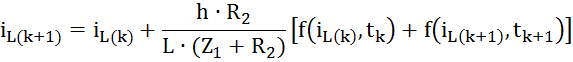
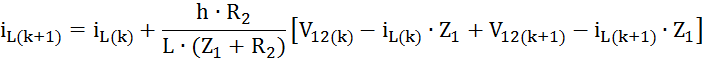
Получим выражение для определения тока на (к + 1)-м шаге:

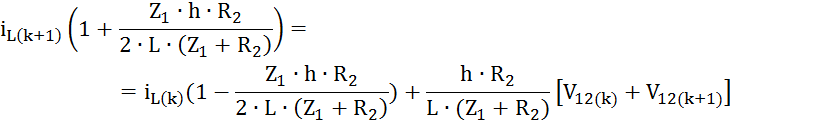
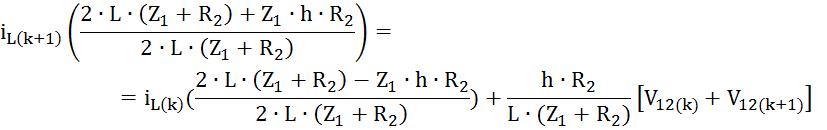
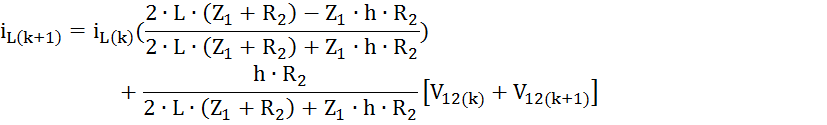
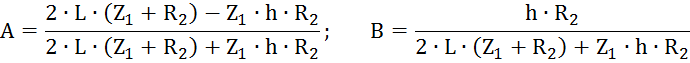
Распечатка программы разработанного алгоритма

% Исходные данные

tr=60.e-6;               %- время расчета                        

h=0.1e-6;                %- шаг расчета       

D1=1800;D2=10.e8;        %- длина ВЛ и КЛ         

v1=150.e6;v2=300.e6;     %- скорости распр. волн по ВЛ и КЛ             

Z1=40;Z2=40;             %- волновые сопротивления ВЛ и КЛ

Z=40;                    %- сопротивление источника

R1=80;                   %- активное сопротивление нагрузки в узле 2

R2=26.67;                %- эквивалентное активное сопротивление нагрузки в узле 3

L=0.5e-4;                 %- индуктивность катушки в узле 3          

U0=1;                    %- амплитуда воздействующей волны 

ti=10.e-6;                %- длительность срезанного импульса

il=0;                    %- начальное значение il(t)   

nt=tr/h;                 %- количество циклов по времени  

% Начальные значения массивов напряжений и времени

UM1=0;UM2=0;UM3=0;tm=0;

% количество шагов по линиям

N1=round(D1/v1/h);

A=(2*L*(R2+Z1)-Z1*h*R2)/(2*L*(R2+Z1)+Z1*h*R2);

B=h*R2/(2*L*(R2+Z1)+Z1*h*R2);

V12=zeros(1,N1);

V21=zeros(1,N1);

% Расчет волнового процесса (цикл по времени)

for k=1:nt

   t=k*h;

   if(t<=ti)

      e=2*U0;

   else                           %- срезанный импульс

    e=0;

      end

%e=2*U0;                            %- прямоуг. импульс

      % Вычисление значений напряжения в узлe 1

      U1=(V21(k)*Z)/(Z+Z1)+(e*Z1)/(Z+Z1);

      W12=2*U1-V21(k);                   % Вычисление отраженной волны от узла 1

      V12(k+N1)=W12;                     % Сдвиг волны V12 на шаге расчета                                   

      % Вычисление значений напряжения в узлe 2

      il=il*A+B*(V12(k)+V12(k+1));      

      U2=((V12(k+1)*R2)/(Z1+R2))-(il*(Z1*R2))/(Z1+R2);

      W21=2*U2-V12(k+1);                 % Вычисление отраженных волн от узла 2

      V21(k+N1)=W21;                     % Сдвиг волны V21 на шаге расчета     

      % Формирование массивов напряжений и времени

      UM1=[UM1 U1];

      UM2=[UM2 U2];

      tm=[tm t*1.e6];

   end

subplot(211),plot(tm,UM1,'blue'),grid; 

title('Расчетные кривые изменения U(t) в узлах')

ylabel('U1(t)')

subplot(212),plot(tm,UM2,'blue'),grid;

ylabel('U2(t)')

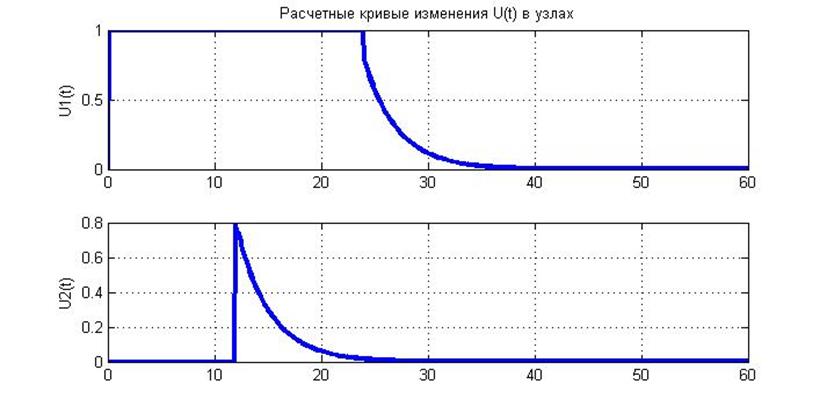
Расчётные кривые изменения напряжения в исследуемых узлах схемы

В случае прямоугольного импульса бесконечной длительности

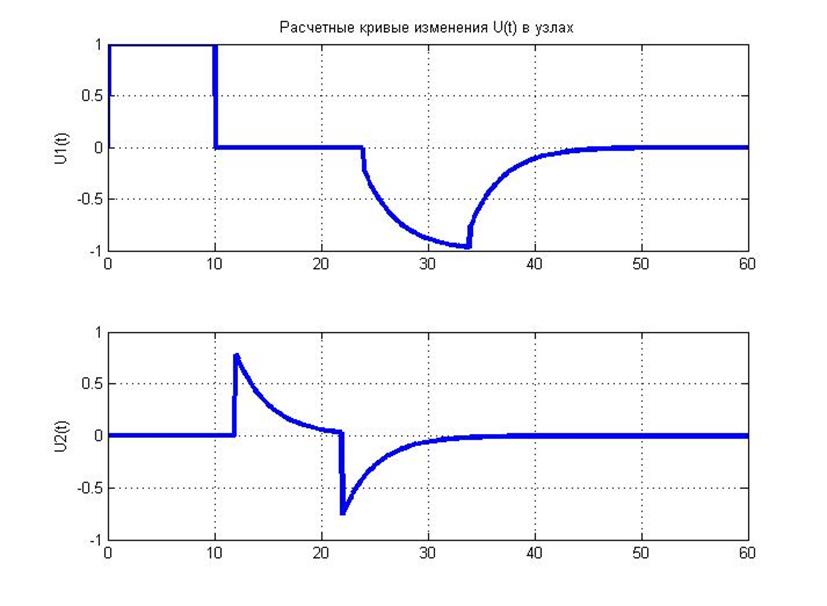
В случае прямоугольного импульса конечной длительности

Выводы:

       При приходе прямоугольной волны бесконечной длительности в узел с сопротивлением и индуктивностью происходит отражение волны от него и её уменьшение по экспоненциальному закону, что объясняется изменением сопротивления индуктивности с течением времени, т.е. она накопила энергию.

      Когда мы имеем дело с прямоугольными волнами конечной длительности, то происходящие процессы по природе аналогичны с теми же что и при прямоугольной волне бесконечной длительности, только они происходят конечное время (длительность импульса) и при этом после окончания импульса сами элементы (индуктивность, ёмкость) отдают запасённую во время импульса энергию.