Исследование линейных цепей несинусоидального тока (Лабораторная работа № 6), страница 8

Это функция с периодом колебаний Т_Ω=. Заменяя произведение двух гармоничес-ких колебании, суммой выражению (6.2) можно придать вид:

               u(t)=U_m(t)sinω₀t=U_0msinω₀t+m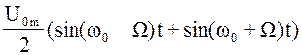           (6.3)

В (6.3) записана сумма трех гармоник, с несущей частотой ω₀ и двух боковых: ω₁ и ω₂.

ω₁=ω₀-Ω,  ω₂=ω₀+Ω. Выражение (6.3) и будем использовать для дальнейшего анализа.

 Рассмотрим последовательную цепь RLC, с АМ источником (рис.6.15). Чтобы

R

C

e(t)

L

i0(t)

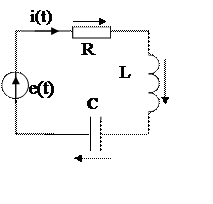
                                                      найти токи и напряжения необходимо, применяя                                       метод наложения, три раза рассчитать схему. Про-                                   анализируем частотные свойства контура, в частно-                                          сти  влияние  ширины пропускания контура на ам-

                                                      плитудно-частотную характеристку  (АЧХ) и фазо                                            -частотную характеристку (ФЧХ) комплексного Рис.6.15 Схема RLC с AM -э.д.с    коэффициента передачи по напряжению К(jω).

                                                            Комплексный коэффициент передачи определяют как:

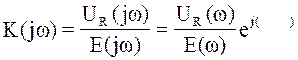                                                                            (6.4)

- амплитудно-частотная характеристика,

  φ_R-φ_E  =  φ(ω)-  фазо-частотная характеристика.

Приведенные выражения показывают: для определения K(jω) требуется провести расчет схемы для разных значении угловой частоты ω. Так как, э.д.с. содержит три гармоники, то расчет следует сделать трижды.

Получим выражение для K(jω) на основной (несущей) частоте. Расчетная схема приведена на рис.6.16.

UR(0)

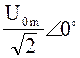                                                             Е⁽⁰⁾=- комплекс э.д.с. на основной частоте      

                                                                          jX_L⁽⁰⁾=jω₀L; - jX_C⁽⁰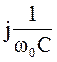⁾=-;  U_R⁽⁰⁾= I ⁽⁰⁾R                                                                                                                               

         Рис.6.16.Расчетная схема                      I⁽⁰⁾ =  =

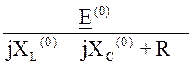
    K(jω₀)==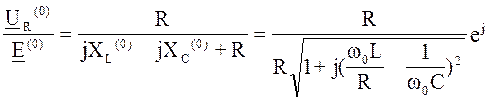

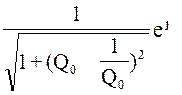
Q₀- значение добротности  контура на основной (несущей)  частоте

   К(ω₀)=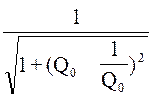- величина АЧХ на основной (несущей)  частоте.

φ₀= arctg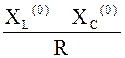- величина ФЧХ на основной (несущей) частоте.

Аналогично определяются значения ФЧХ и АЧХ на боковых частотах. Обе характеристики зависят от частоты и параметров контура (R,L,C). При заданном значении ω₀ повлиять на поведение К(ω) и φ(ω) можно подбором параметров (R,L,C), исходя из заданных требовании к K(jω).

Это главные сведения, которые Вам потребуются при выполнении третьего опыта.

Б.Расчетная подготовка к проведению эксперимента

Задание: Подобрать величину R,L,С при следующих условиях:

                а) при ω=ω₀ (основная частота) К(ω₀) имеет максимальное значение

                б) ширина полосы пропускания контура равна разности боковых частот

Полученные значения R,L,C и Q₀ внесите в таб.6.8.

Примечание: Величину одного из параметров (R, L, или С) возьмите по усмотрению.

          В. Сборка схемы.

Экспериментальная схема для исследования спектра амплитудно-модулированного источника э.д.с. приведена на (рис 6.18,а). Этот элемент находится на панели исто- чников. Панель параметров показана на (рис.6.17).

моделирующая частота

коэффициент модуляции

несущая частота

среднее значение напряжение

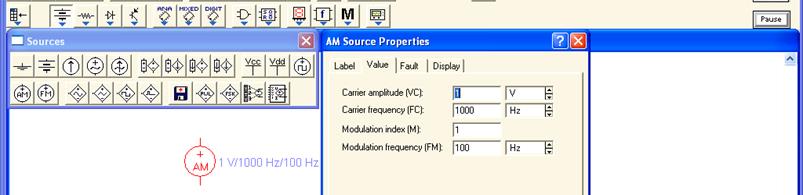
                          Рис.6.17. Амплитудно-модулированный источник

Величину параметров источника установить, согласно номеру варианта (таб.6.8).