Исследование линейных цепей несинусоидального тока (Лабораторная работа № 6), страница 5

Форма э.д.с.	КОЭФФИЦИЕНТЫ
	амплитуды	формы	гармоник	искажения
Синус
Треугольник
Прямоугольник

 Примечание. Картинку по рис.6.9 можно получить и другим способом. После того  как появилась вспомогательная панель (рис.6.8), щелкните левой кнопкой “мыши” на строке Properties, появиться панель Graph Properties , расставив галочки на ней можно построить координатные сетки, вызвать измерительные курсоры. Эти действия надо проделать для каждого графика отдельно. В результате Ваших действ-

ий на экране должна появиться следующая картинка (рис.6.10). Затем убрать панель Graph Properties, нажав кнопку ”OК”.

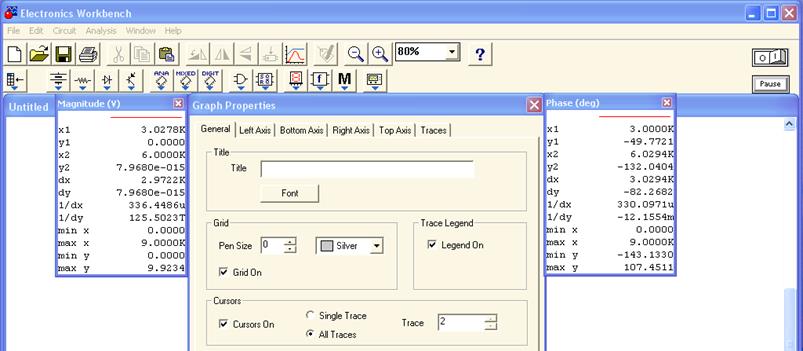
                          рис.6.10. Использование панели Graph Properties  

Примечание: Вопросы для зачета по 1^ой схеме в конце 6-ой лабораторной работы.

Приступим к выполнению пункта №2:

2.ИССЛЕДОВАНИЕ ЦЕПИ R,L,C НЕСИНУСОИДАЛЬНОГО ТОКА.

A.Теоретические сведения.

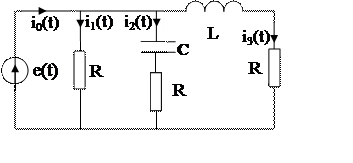
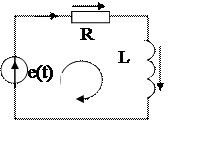
                                             Исходная схема имеет вид (рис.6.11). Обсудим расчет этой схемы. В схеме два узла, четыре ветви, три контура. Следовательно, можно со- ставить одно уравнение по 1-ому закону Кирхгофа и три по 2-ому:       

                                                                              

                                                                                  i₀(t)=i₁(t)+i₂(t)+i₃(t),

                                                                                        i₁(t)R = e(t),

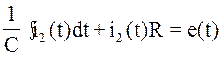                                                               ,              (6.1)

     рис.6.11.Исходная схема                           .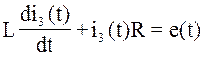                    

Метод решения системы уравнении (6.1) зависит от двух факторов: во-первых какой режим рассчитывается: переходный или установившийся; во-вторых какой вид имеет э.д.с. е(t). В данной работе будем рассчитывать установившийся режим, когда  э.д.с. е(t) периодическая несинусоидальная функция. В этом случае следует получить ряд Фурье для э.д.с. той или иной формы (таб.6.1) и последовательно рассчитать схе-му отдельно от каждой гармоники. Пусть ряд Фурье для э.д.с. е(t) имее вид:

             е(t)=E⁽⁰⁾+E_m⁽¹⁾sin(ω₁t+φ₁)+ E_m⁽²⁾sin(ω₂t+φ₂)+ E_m⁽³⁾sin(ω₃t+φ₁)+……

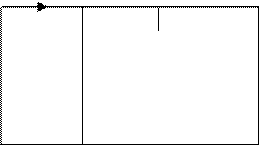
Используя метод наложения, рассчитываем от нулевой гармоники: Е⁽⁰⁾.  Расчет- ная схема показана на (рис.6.12).

I3(0)

I1(0)

I0(0)

UC(0)

Е(0)

R

R

                                                              I₁⁽⁰⁾=     I₃⁽⁰⁾=    I₀⁽⁰⁾= I₁⁽⁰⁾+ I₃⁽⁰⁾

R

                                                                   U_C⁽⁰⁾= E⁽⁰⁾

                                                                     P_Г⁽⁰⁾= E⁽⁰⁾ I₀⁽⁰⁾

     Рис.6.12. Расчетная схема

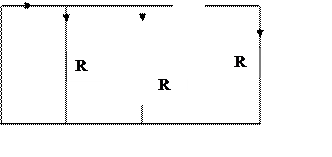
Далее ведем расчет от действия 1-ой гармоники. Так как при этом имеем дело с  синусоидальной э.д.с. и рассматривается установившийся режим, то следует примен-ить символический метод. Расчетная схема показана на рис.6.13.

I1(1)

I0(1)

I2(1)

jXL(1)

                                                           Очевидно, все ветви соединены параллель-                    

I3(1)

                                                               но. Во 2-ой лабораторной работе Вы учились