Одномерная минимизация функций, страница 2

Отсюда: .

Проверяем условие : . Условие не выполняется. Следовательно процесс вычисления продолжается в соответствии с приведенным алгоритмом до достижения точности .

Метод золотого сечения

Находим

 

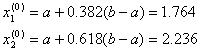
Вычисляем значения :

.

Сравниваем значения : .

Отсюда: .

Вычисляем .

Проверяем условие : . Условие не выполняется, значит, переходим к следующей итерации.

Сравниваем значения : .

Отсюда: .

Вычисляем .

Проверяем условие : . Условие не выполняется, значит процесс вычисления продолжается в соответствии с приведенным алгоритмом до достижения точности .

Результат работы программы:                     График функции на интервале:

 

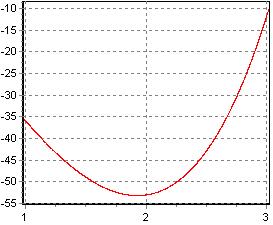min F(x) = F(1.92627) = -53.1459  x Result was find in 11 iterations

Вывод: В ходе лабораторной работы была разработана программа для одномерной минимизации функции методом дихотомии. Реализованный метод оказался довольно эффекимвным. Решение данной задачи методом золотого сечения заняло бы 15 итераций. Метод так же хорош при нахождении минимума с большой точностью. При уменьшении погрешности в 2 раза, количество итераций взрастает всего на одну.