














Министерство высшего и среднего специального образования
РСФСР
Сибирский ордена Трудового Красного Знамени металлургический институт имени Серго Орджоникидзе
Использование электронного осциллографа для изучения периодических процессов.
Методические указания к выполнению лабораторной работы по курсу «Общая физика»
Издание СМИ Новокузнецк 1987
Краткая теория.
1. Сложение взаимно перпендикулярных колебаний.
Фигуры Лиссажу
Допустим, что колебания некоторой точки вдоль осей x и у описываются уравнениями
x=aCosωt,
y=bCos(ωt+a) (1)
где a и b- амплитуды колебаний; ω – частота; a - равность фаз колебаний.
Движение точки в этом случае будет происходить, вообще говоря, по криволинейной траектории, форма которой зависит в основном от разности начальных фаз.
Уравнения (I) представляет собой заданное в параметрической форме уравнение траектории, по которой движется точка, участвующая в обоях колебаниях. Чтобы получить уравнение траектории я явном виде, нужно исключить ив уравнений (I) время t как параметр. В результате получим:
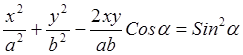 (2)
(2)
Исследуем форму траектории для частных случаев:
а) α=0 В атом случае
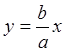 (3)
(3)
уравнение
прямой. Результирующее движение является гармоническим колебанием вдоль этой
прямой с частотой ω и амплитудой, равной ![]() ;
;
б) a=± π Подставляя в формулу(2), получим:
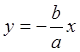 ,
(4)
,
(4)
т.е. траектория также представляет собой прямую линию;
в) a=± π/2 Уравнение (2) переходит в
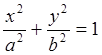 (5)
(5)
т.е. уравнение эллипса, приведенного к координатным осям, причем полуоси эллипса равны соответственно амплитудам колебаний. При равенстве амплитуд a и b эллипс вырождается в окружность.
В случае, когда частоты взаимно перпендикулярных колебаний отличаются на очень малую величину Δω, их можно рассматривать как колебания одинаковой частоты, но с медленно меняющейся разностью фаз. Результирующее движение в этом случае происходит по медленно видоизменяющейся кривой, которая будет последовательно принимать форму, отвечающую всем значениям разности фаз от –π до +π.
Если частоты взаимно перпендикулярных колебаний не одинакова, но кратны, то траектория результирующего движения имеет вид довольно сложных замкнутых кривых, называемых фигурами Лиссажу. На рис.1 показаны фигуру Лиссажу для частот различной кратности и разности начальных фаз.
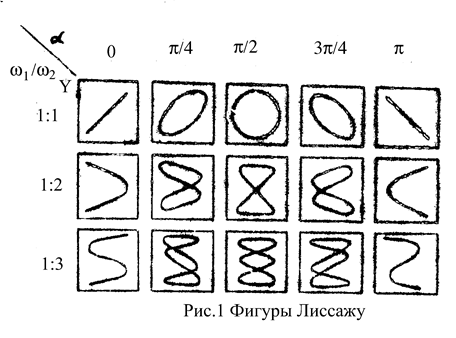 |
2. Вынужденные электромагнитные колебания в контуре
Электромагнитными колебаниями в контурах навиваются периодические изменения силы тока, обусловленные электрическими и магнитными свойствами этих контуров. Всякий реальный электрический контур, т.е. цепь, состоящая из катушки с индуктивностью L и конденсатора емкостью С, обладает активным сопротивлением. Энергия контура постепенно убывает за счет выделения тепла на активном сопротивлении. Вследствие этого колебания в контуре затухают.
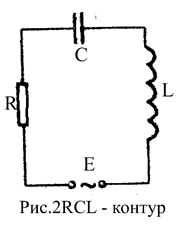 |
Уравнение вынужденных колебаний для такого контура можно получить исходя из того, что сумма падений напряжения на емкости, индуктивности и активном сопротивлении должна быть равна внешней ЭДС:
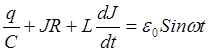 (6)
(6)
где
q- заряд на пластинах конденсатора; J
- сила тока, протекающего по контору;
ε0 - ЭДС внешнего источника, изменяющаяся со временем по
гармоническому закону (![]() ).
).
Дифференцируя это уравнение по времени и используя 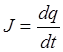 получим:
получим:
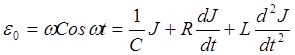 (7)
(7)
Решение этого уравнения имеетвид:
![]() (8)
(8)
где
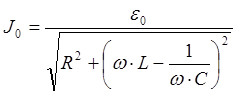 (9)
(9)
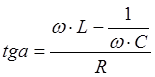 (10)
(10)
Здесь:
Jo - амплитудное значение силы тока; ωL
- индуктивное сопротивление контура; ![]() - емкостное сопротивление контура;
- емкостное сопротивление контура;
a - сдвиг фаз между внешней ЭДС и током в контуре.
Максимальное значение силы тока достигается при
условии 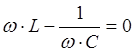 , т.е. при
, т.е. при 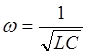 (11)
(11)
Зависимость амплитуды установившихся колебаний от частоты
внешнего напряжения носит название резонансной кривой. Частота, соответствующая
максимуму резонансной кривой, называетсярезонансной частотой.
Следовательно, резонансная частота 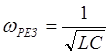 , т.е.
совпадает с собственной частотой контура ω0. Таким образом,
для тока резонансная частота не зависит от активного сопротивления R ; от R зависит лишь крутизна и ширина резонансной кривой.
, т.е.
совпадает с собственной частотой контура ω0. Таким образом,
для тока резонансная частота не зависит от активного сопротивления R ; от R зависит лишь крутизна и ширина резонансной кривой.
Ширина резонансной кривой определяет важнейшую характеристику контура - его добротность. Добротность показывает, во сколько paз запасенная в контуре энергия превосходит среднюю величину энергии, теряемой контуром за время, в течение которого фаза колебаний изменяется на 1 радиан. Ширина кривой и добротность контура Q, связаны соотношением
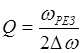 (12)
(12)
Величина
2∆ω измеряется на уровне ![]() , где АMAX -максимальная
амплитуда, соответствующая резонансной частоте
, где АMAX -максимальная
амплитуда, соответствующая резонансной частоте
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.