Для
определения аппроксимирующего полинома требуется подобрать коэффициенты ![]() таким образом, чтобы величина S
была минимальной.
таким образом, чтобы величина S
была минимальной.
Коэффициенты
![]() определяются в результате решения
следующей системы линейных уравнений:
определяются в результате решения
следующей системы линейных уравнений:
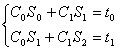 , где
, где
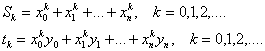 , причем
, причем ![]() .
.
Полином
с коэффициентами ![]() будет обладать минимальным
квадратичным отклонением
будет обладать минимальным
квадратичным отклонением ![]() .
.
Результат работы программы: График, построенный по полиному:
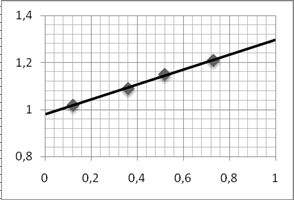 |
|
Approximated function is: Q(x)=0.98101+0.315585*x Smin=4.83988e-005 |
Вывод:
В ходе лабораторной работы была
разработана программа для вычисления коэффициентов аппроксимации минимального
квадратичного отклонения ![]() . Реализованый метод оказался очень точным,
т.к. отклонение не превышает 5*10-5. Также при нахождении полинома
первуй степени не требуется мощных вычислительных ресурсов.
. Реализованый метод оказался очень точным,
т.к. отклонение не превышает 5*10-5. Также при нахождении полинома
первуй степени не требуется мощных вычислительных ресурсов.
Расчетное задание
Требуется для исходной функции записать полином Лагранджа.
![]()
![]()
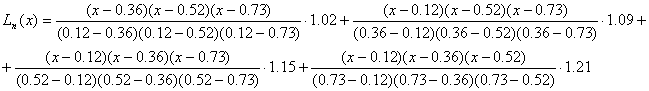
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.