Проверка гипотез. Представление результатов проверки статистических гипотез в публикациях, страница 5

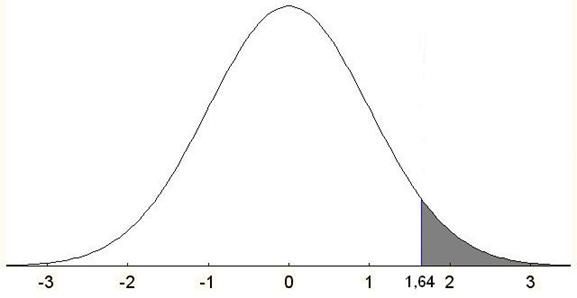
Рис. 2. Распределение выборочной статистики (в стандартных оценках) для направленной альтернативной гипотезы и α = 0,05.

Поскольку вся 5%-ая критическая область располагается на одном конце выборочного распределения, критическая значение сдвигается в сторону μ. Для уровня значимости α = 0,05 и для направленной альтернативной гипотезы критическое значение составляет примерно 1,64[3]. Поэтому односторонние критерии (правила принятия решения, такие как нормальное распределение, – one-tailed tests) более чувствительны к имеющимся различиям или, как предпочитают говорить статистики, обладают большей мощностью. Несмотря на это, двусторонние критерии (two-tailed tests) используются чаще. Одна из причин тем, что исследователь не всегда располагает убедительной и надежной теорией, предсказывающей направление результатов. Кроме того, исследователи часто пытаются застраховать себя от нежелательных выводов. Например, если бы в силу случайной ошибки или по содержательным причинам, которыми пренебрегают в психологической литературе, в выборке первенцев уровень интеллекта оказался бы равным 92 пунктам, мы не смогли бы отклонить нуль-гипотезу в пользу направленной гипотезы μ > μ₀. Заметьте, что этот совершенно неожиданный результат интересен и мог бы привести к разработке новой теории, например, о том, что повышенные ожидания и требования родителей к первенцам способствуют приобретению тривиальных знаний и навыков, но мешают развитию творческих способностей.

В статистической методологии продолжается спор о том, можно ли сочетать односторонние и двусторонние критерии. Например, некоторые исследователи сначала проверяют значимость результата с помощью более мощного одностороннего критерия и затем, в случае получения статистически значимой разности с другим, чем ожидалось, знаком, используют более осторожный двусторонний критерий. Другие исследователи сначала используют двусторонний критерий, а после подтверждения значимости результата и проверки его направленности – соответствующий односторонний. В обоих случаях альтернативная гипотеза меняется в ходе проверки гипотезы. Традиционная статистическая методология считает подобную практику некорректной. По существу, в обоих случаях осуществляются две проверки, каждая из которых имеет риск неверного решения (α и α/2), поэтому общая ошибка I рода увеличивается в полтора раза.

В заключение приводим критические значения для нормального стандартного распределения (табл.2).

Таблица 2

Критические значения одностороннего и двустороннего критерия z (стандартное нормальное распределение) для нескольких уровней значимости

Представление результатов проверки статистических гипотез в публикациях

В научных статьях и отчетах принято указывать не только сам результат проверки («различия статистически значимы»), но и некоторую более общую информацию о процедуре проверки. Например, следует указывать название (или общепринятый символ) использованного статистического критерия. Сейчас вы знакомы только с нормальным распределением (и z-критерием), но статистических методов довольно много: критерии t, F, χ², Тьюки, Шеффе, Уэлша, Ливина, Колмогорова-Смирнова и др. С некоторыми критериями мы познакомимся в следующих темах. Далее, необходимо указывать значение этих критериев и некоторую специфическую информацию, важную для их интерпретации[4]. Наконец, следует указать уровень статистической значимости, например, «p < 0,01» (ноль перед запятой обычно опускается). Уровень значимости результатов, представленных в табличной форме, часто указывают с помощью звездочек (*). Конечно, вам придется учитывать сложившуюся практику. В нашей стране некоторые редакторы журналов возражают против приведения численных значений статистических критериев, аргументируя это тем, что техническая информация усложняет понимание текста.