Математика \ Вычислительная математика

Решение систем линейных алгебраических уравнений, страница 2

МЕТОД ГАУССА:

3.1629

2.0129

8.2101

5.5512

3.2229

МЕТОД НАИСКОРЕЙШЕГО СПУСКА:

с начальными условиями х(i)=0, i=1,n

k

x(1)

x(2)

x(3)

x(4)

x(5)

1

2.5866

2.1595

5.9561

5.0848

5.7689

2

2.7748

1.7413

7.8988

5.7582

3.2418

3

2.9898

2.0506

8.2059

5.6938

3.4255

4

3.1249

2.0084

8.2352

5.5409

3.2357

5

3.1523

2.0161

8.2078

5.5573

3.2361

6

3.1607

2.0117

8.2111

5.5510

3.2240

7

3.1621

2.0132

8.2101

5.5517

3.2237

8

3.1628

2.0128

8.2102

5.5511

3.2231

9

3.1629

2.0129

8.2101

5.5512

3.2230

10

3.1629

2.0129

8.2101

5.5512

3.2230

с начальными условиями х(i)= b(i)/a(i,i), i=1,n

k

x(1)

x(2)

x(3)

x(4)

x(5)

1

3.1510

1.8115

7.7910

5.7215

3.2276

2

3.1417

2.0456

8.2040

5.6223

3.2946

3

3.1480

2.0108

8.2187

5.5564

3.2284

4

3.1611

2.0160

8.2099

5.5533

3.2280

5

3.1619

2.0126

8.2100

5.5512

3.2237

6

3.1627

2.0131

8.2101

5.5515

3.2233

7

3.1628

2.0128

8.2102

5.5512

3.2230

8

3.1629

2.0129

8.2101

5.5512

3.2230

МЕТОД ЗЕЙДЕЛЯ:

с начальными условиями х(i)=0, i=1,n

k

x(1)

x(2)

x(3)

x(4)

x(5)

1

4.0000

1.7832

7.0711

5.3688

3.0356

2

3.2068

2.0094

8.1853

5.5386

3.2076

3

3.1666

2.0127

8.2088

5.5501

3.2215

4

3.1633

2.0129

8.2100

5.5511

3.2228

5

3.1630

2.0129

8.2101

5.5512

3.2229

6

3.1629

2.0129

8.2101

5.5512

3.2229

с начальными условиями х(i)= b(i)/a(i,i), i=1,n

k

x(1)

x(2)

x(3)

x(4)

x(5)

1

2.6382

1.9226

8.0055

5.7628

3.4863

2

3.0968

2.0152

8.2322

5.5702

3.2486

3

3.1569

2.0130

8.2118

5.5530

3.2253

4

3.1624

2.0129

8.2103

5.5514

3.2232

5

3.1629

2.0129

8.2102

5.5512

3.2230

6

3.1629

2.0129

8.2101

5.5512

3.2229

Таблица 2

Сходимость оценки корня к истинному значению

Метод Гаусса

Метод Зейделя

Метод наискорейшего спуска

k

x(1) н.у.х=0

x(1) н.у. х=β

x(1) н.у.х=0

x(1) н.у. х=β

1

3.1629

4.0000

2.6382

2.5866

3.1510

2

3.1629

3.2068

3.0968

2.7748

3.1417

3

3.1629

3.1666

3.1569

2.9898

3.1480

4

3.1629

3.1633

3.1624

3.1249

3.1611

5

3.1629

3.1630

3.1629

3.1523

3.1619

6

3.1629

3.1629

3.1629

3.1607

3.1627

7

3.1629

3.1629

3.1629

3.1621

3.1628

8

3.1629

3.1629

3.1629

3.1628

3.1629

9

3.1629

3.1629

3.1629

3.1629

3.1629

Рисунки функций

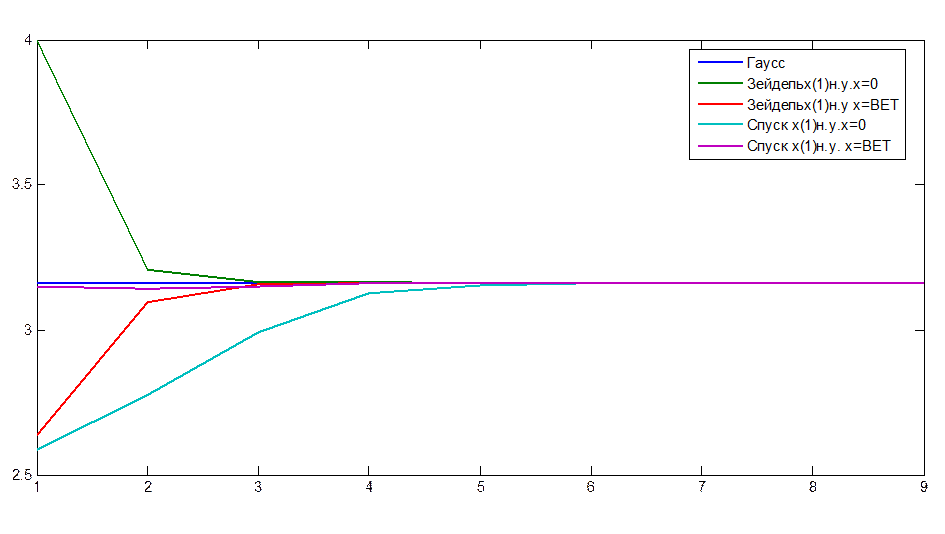Рисунок1

На рисунке 1 изображены графики сходимости корня   итерационных методов в виде  (k - номер итерации) для   и .

Вывод

В ходе работы мы убедились, что для данной постановки задачи результат метода Зейделя быстрее сходится к истинному значению.


Приложение

Листинг программы

a=[0.380  -0.050  0.010  0.020  0.070

0.052   0.595   0.000   -0.040 0.040

0.030   0.000   0.478   -0.140 0.080

0.060   0.126   0.000   0.470  -0.020

0.250   0.000   0.090   0.010  0.560]

b=[  1.520;      - 1.269;          3.500;     - 2.988;       3.390]

e=0.0001;

for i=1:5

   x1(i)=b(i)/a(i,i);

   x2(i)=b(i)/a(i,i);

end

n=5;

x=n1ygau(a,b,n)

k=1;

[x1,g]=n1ymgs(a,b,x1)

xx1(1)=x1(1);

while norm(g,2)>e

    k=k+1;

   [x1,g]=n1ymgs(a,b,x1)

   xx1(k)=x1(1);

end

for i=1:k

    kk1(i)=i;

end

k=1

 [x2,g]=n1ymns(a,b,x2)

  xx2(1)=x2(1); 

while norm(g,2)>e  

   k=k+1

   [x2,g]=n1ymns(a,b,x2)

    xx2(k)=x2(1);

end

for i=1:k

    kk2(i)=i;

end

%-------------------------------------------

for i=1:5

    x11(i)=0;

    x21(i)=0;

end   

k=1

xx11(i)=x11(1);

[x11,g]=n1ymgs(a,b,x11)

while norm(g,2)>e

    k=k+1;

     [x11,g]=n1ymgs(a,b,x11)

     xx11(k)=x11(1);

 end

 for i=1:k

     kk11(i)=i;

 end

 k=1

  xx21(1)=x21(1);

  [x21,g]=n1ymns(a,b,x21)  

 while norm(g,2)>e

     k=k+1

     [x21,g]=n1ymns(a,b,x21)

xx21(k)=x21(1);

end

for i=1:k

kk21(i)=i;

end

Скачать файл