



МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра Автоматики
Расчетно-графическая работа №2
Вариант 16
|
Факультет: АВТ Группа: АА-86 Студент: Сапрыкин О.Н. |
Преподаватель: Каменский С.В. |
Дата выполнения: __.05.2011
Отметка о защите:
Новосибирск
2011
Задание:
|
16 |
M |
n |
k |
d |
D |
№ сообщения |
||||||||
|
2-10 8-7-2-1 |
820 |
? |
? |
? |
? |
137 |
||||||||
|
КГ |
? |
? |
8 |
? |
? |
130 |
||||||||
|
КЗП |
220 |
? |
? |
? |
? |
142 |
||||||||
|
МКХ |
? |
? |
6 |
? |
? |
59 |
? |
? |
- |
- |
- |
- |
х7 |
? |
|
ЦК |
2000 |
? |
? |
? |
? |
1617 |
5 |
5 |
- |
- |
? |
? |
х20 |
? |
|
M |
n |
k |
d |
D |
№ сообщения |
r |
s |
P |
H |
p(x) |
h(x) |
E(x) |
S(x) |
|
![]() [1] (в конце представлен
список литературы)
[1] (в конце представлен
список литературы)
![]()
![]()
![]()
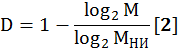
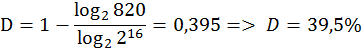
![]()
![]()
![]()
Для получения кода Грея сложим по модулю два исходное число в двоичном коде с числом, циклически сдвинутым вправо на один разряд:
![]()
![]()
![]()
![]()
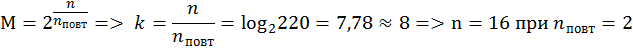
![]()
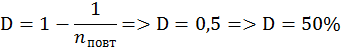
При кодировании с защитой
повторением исходная комбинация передается несколько раз подряд, то есть ![]() будет передано как
будет передано как ![]()
В данном коде контрольные символы располагаются на позициях с номером 2i, где i = 0,1,2,…
![]() , n – длина комбинации.
, n – длина комбинации.
Так
как число информационных символов равно 6, то число контрольных символов равно 4,
а длина n=10 ![]()
![]()
![]() [4]
[4]
![]()
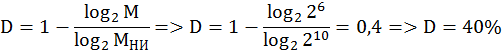
Запишем представление сообщения в классическом КХ:
a1 a2 a3 a4 a5 a6 a7 a8 a9 a10, где a1, a2, a4, a8 – контрольные символы, а остальные – информационные.
Запишем уравнения проверок по известному правилу (“с первого по одному через один”, “со второго по два через два и т.д.”):
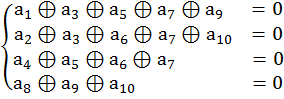
В МКХ добавляется еще один контрольный символ общей проверки на четность (a15), запишем для него уравнение проверок:
![]()
Разрешим уравнения относительно контрольных символов:
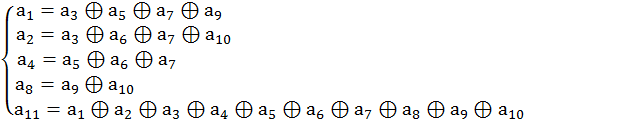
![]()
|
a1 |
a2 |
a3 |
a4 |
a5 |
a6 |
a7 |
a8 |
a9 |
a10 |
|||||
|
_ |
_ |
1 |
_ |
1 |
1 |
0 |
_ |
1 |
1 |
|||||
Рассчитаем контрольные символы:

|
a1 |
a2 |
a3 |
a4 |
a5 |
a6 |
a7 |
a8 |
a9 |
a10 |
|||||
|
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|||||
![]()
|
a1 |
a2 |
a3 |
a4 |
a5 |
a6 |
a7 |
a8 |
a9 |
a10 |
a11 |
||||
|
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
||||
Декодирование: ![]() , значит, принятая комбинация имеет вид:
, значит, принятая комбинация имеет вид:
|
a1 |
a2 |
a3 |
a4 |
a5 |
a6 |
a7 |
a8 |
a9 |
a10 |
a11 |
||||
|
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
||||
Рассчитаем синдром Хэмминга и синдром ОПЧ:
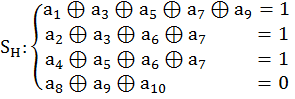
![]()
![]()
Т.к. ![]() а
а ![]() , то ошибка двойная, коррекции нет,
декодирование запрещено [5]
, то ошибка двойная, коррекции нет,
декодирование запрещено [5]
![]()
![]() => т.к.
=> т.к. ![]() – это БЧХ код
– это БЧХ код
![]() [6]
[6]
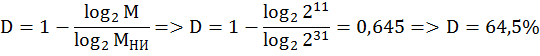
P(x) → 5423325 → 101 100 010 011 011 010 101 → x20+x18+x17+x13+x10+x9+x7+x6+x4+x2+1
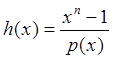 [7]
[7]
![]()
![]() =>
=> ![]()
![]() , где
, где ![]() [8]
[8]
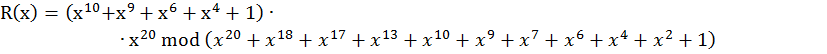
![]()
![]()
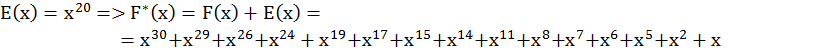
Неселектируемый синдром:
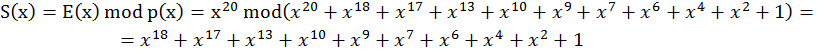
Селектируемый синдром:
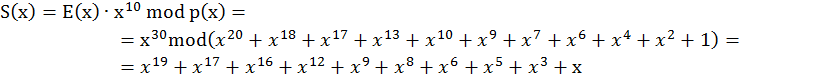
Список литературы:
1. Телемеханика. Учеб. пособие для вузов по спец. "Автоматика и телемеханика" В. Н. Тутевич, 1989
[1] стр 6 [3] стр 70
[2] стр 5 [6] стр 87
2. Кодирование сообщений методические указания к лабораторным работам для 3-5 курсов АВТФ (специальностей 210100 и 220400) всех форм обучения Новосиб. гос. техн. ун-т ; [сост.: А. Б. Жуков, С. В. Каменский], 2003
[4] стр 36 [7] стр 49
[5] стр 37 [8] стр 50
3. Конспект лекций
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.