Работа со сплайнами в Spline Toolbox
Область применения сплайнов весьма широка: они используются при аппроксимации одномерных и многомерных данных и функций, во многих других вычислительных задачах, а также в двумерной и трехмерной графике. Средства Spline Toolbox позволяют конструировать одномерные и многомерные сплайны (как интерполяционные, так и сглаживающие), удовлетворяющие различным условиям гладкости, и применять их для решения разнообразных задач. Входящие в состав Toolbox приложения с графическим интерфейсом служат для получения наглядного представления о поведении сплайнов и экспериментов с ними.
Сплайны и формы их представления
Рассмотрим сначала задачу приближения табличной функции одной переменной с помощью сплайнов. Напомним основные определения и термины. Для решения задачи должны быть заданы две последовательности: точки х1, х2, xN (сетка) и значения аппроксимируемой функции в этих точках y1, у2,… yN (сеточная функция). Сетка считается упорядоченной, т.е. x1 < хi+1. Если аппроксимирующая функция проходит через заданные точки-то она называется интерполирующей, а иначе — сглаживающей. Функция S(x) называется сплайном степени k-1 (порядка k), если на каждом, отрезков [xi, xi+1], где i = 1, 2,…,N-1, эта функция является полином степени не выше к-1. Точки хi (i=2,..., N — 1) называются точками разрыва, в них полиномы "сшиваются" так, что сохраняется непрерывное производной некоторого порядка di <k-1 (в разных точках условия гладкости могут быть различными). Используются две основные формы представления сплайна: кусочно-полиномиальная (рр-форма) и В-форма, выражающая сплайн через базисные сплайны.
Примечание
В русскоязычной литературе вместо термина "точки разрыва", как правило, используется термин "узлы". Мы будем придерживаться терминологии, принятой в пакете MATLAB.
Кусочно-полиномиальная форма (рр-форма)
На каждом участке [хj,хj+1] с номером j приближающая функция S(х) представляется в виде полинома
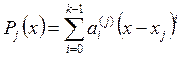
рр-форма удобна для вычисления значений сплайна, его дифференцирования, интегрирования и других операций с ним. Построение сплайнов в рр-форме, т. е. определение множества коэффициентов, сопряжено с решением системы линейных уравнений и изменение любого значения в табличных данных требует пересчета всех коэффициентов.
В-форма
(разложение по базисным сплайнам)
B-форма опирается на понятие базисных сплайнов. Несколько менее очевидный смысл их представления (по сравнению с рр-формой) компенсируется тем, что внесение изменений в табличные данные требует меньшего объема вычислений для перестроения сплайна. Сплайн в В-форме представляется суммой
s(x) = 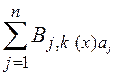
где k — порядок сплайна; Bj,к(х) — базисные сплайны (В-сплайны); aj — массив коэффициентов; k — порядок сплайна. Отметим, что базисный сплайн Bj,к(х) положителен и отличен от нуля только в промежутке (tj,tj+k),который называется носителем сплайна. Также выполняется
условие нормировки: 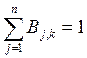 для x [tk, tn+l]. Каждый j-ый базисный сплайн, в свою очередь,
является кусочно-полиномиальной функцией степени меньше kсточками разрыва tj,tj+k . Последовательность точек t1 ≤ t2 ≤ ... ≤ tn+k называется узлами B-формы.
для x [tk, tn+l]. Каждый j-ый базисный сплайн, в свою очередь,
является кусочно-полиномиальной функцией степени меньше kсточками разрыва tj,tj+k . Последовательность точек t1 ≤ t2 ≤ ... ≤ tn+k называется узлами B-формы.
Для обеспечения единственности сплайна заданных условий гладкости в точках разрыва и значений сеточной функции, как правило, недостаточно, поэтому дополнительно задают еще условия на концах рассматриваемого отрезка [х1, xN] —граничные (краевые) условия.
Интерполяционные сплайны
Мы уже обсуждали аппроксимацию функций одной и нескольких переменных средствами MATLAB (см. разд. "Интерполирование и сглаживание" главы 6).
Обратимся теперь к рассмотрению возможностей, предоставляемых Spline Toolbox, и обсудим построение интерполяционных сплайнов, отличающихся порядками, формой представления и граничными условиями. Интерполяционный сплайн S(x) строится таким образом, чтобы для таблично
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.