Число информационных символов: k = 8 → длина кода n = k + 4 = 12
r = s = 1 → кодовое расстояние d = 1 + r + s = 3
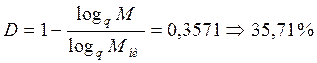
Кодирование сообщения №209: [209]10 → [11010001]2;
Проверочные символы располагаются на позициях с номерами 1, 2, 4, 8, на остальных позициях располагаются информационные символы:
|
a1 |
a2 |
a3 |
a4 |
a5 |
a6 |
a7 |
a8 |
a9 |
a10 |
a11 |
a12 |
|
_ |
_ |
1 |
_ |
1 |
0 |
1 |
_ |
0 |
0 |
0 |
1 |
Записываем уравнения проверок:
i=0, 20=1, получаем “с первого по одному через один”;
a1Åa3Åa5Åa7Åa9Åa11=0;
i=1, 21=2, получаем “со второго по два через два”;
a2Åa3Åa6Åa7Åa10Åa11=0;
i=2, 22=4, получаем “с четвёртого по четыре через четыре”;
a4Åa5Åa6Åa7Åa12=0;
i=3, 23=8, получаем “с восьмого по восемь через восемь”;
a8Åa9Åa10Åa11Åa12=0;
Разрешая уравнения относительно контрольных символов получим уравнения кодирования и подставляя значения информационных символов, найдём a1, a2, a4, a8:
![]() a1=a3Åa5Åa7Åa9Åa11;
a1=a3Åa5Åa7Åa9Åa11;
a2=a3Åa6Åa7Åa10Åa11;
a4=a5Åa6Åa7Åa12;
a8=a9Åa10Åa11Åa12;
![]() a1=
1 Å 1 Å 1 Å 0 Å 0;
a1=
1 Å 1 Å 1 Å 0 Å 0;
a2= 1 Å 0 Å 1 Å 0 Å 0;
a4= 1 Å 0 Å 1 Å 1;
a8= 0 Å 0 Å 0 Å 1;
![]() a1
= 1;
a1
= 1;
a2 = 0;
a4 = 1;
a8 = 1;
Подставляем значение контрольных символов:
|
a1 |
a2 |
a3 |
a4 |
a5 |
a6 |
a7 |
a8 |
a9 |
a10 |
a11 |
a12 |
|
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
Е(х) = х4 → допустим, что исказилась 8-ая позиция и получили
|
a1 |
a2 |
a3 |
a4 |
a5 |
a6 |
a7 |
a8 |
a9 |
a10 |
a11 |
a12 |
|
1 |
0 |
1 |
1 |
1 |
0 |
|
0 |
0 |
0 |
0 |
1 |
Вычислим синдром ошибки по уравнениям проверок:
![]()
![]() a1Åa3Åa5Åa7Åa9Åa11=0 ;
a1Åa3Åa5Åa7Åa9Åa11=0 ;
a2Åa3Åa6Åa7Åa10Åa11=0;
![]() a4Åa5Åa6Åa7Åa12=0;
a4Åa5Åa6Åa7Åa12=0;
a8Åa9Åa10Åa11Åa12=1;
S = [1000]2 → [8]10
Т.е. искаженная позиция найдена и ошибка может быть исправлена.
5) ЦК При заданном числе информационных символов k = 16 и избыточности кода D=0,48, закодировать сообщение №980, циклическим кодом. Если число обнаруживаемых ошибок r=3, число корректируемых ошибок d=3, а вектор ошибки Е(х)=х21.
Определить мощность кода M, длину кода n, кодовое расстояние d, порождающий полином р(х), проверочный полином h(x), синдром ошибки S(x).
Определяем число информационных символов: М ≤ 2k → М ≤ 65536;
Кодовое расстояние: d = r + s + 1 = 7, т.к. d ≥ 5 → код БЧХ [5]. Коды БЧХ позволяют обнаружить и исправить любое число ошибок.
Выберем длину слова. Слово может иметь только нечетное число символов.
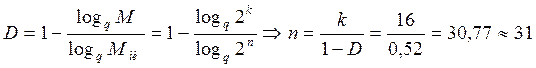
Построения кода БЧХ возможно с помощью таблицы 3.17 [6]
P(x) → 107657 → 001 000 111 110 101 111 → x15+x11+x10+x9+x8+x7+x5+x3+x2+x+1
Получаем код БЧХ (31,16)
Найдем проверочный полином по
формуле : 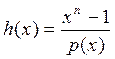 [7]
[7]
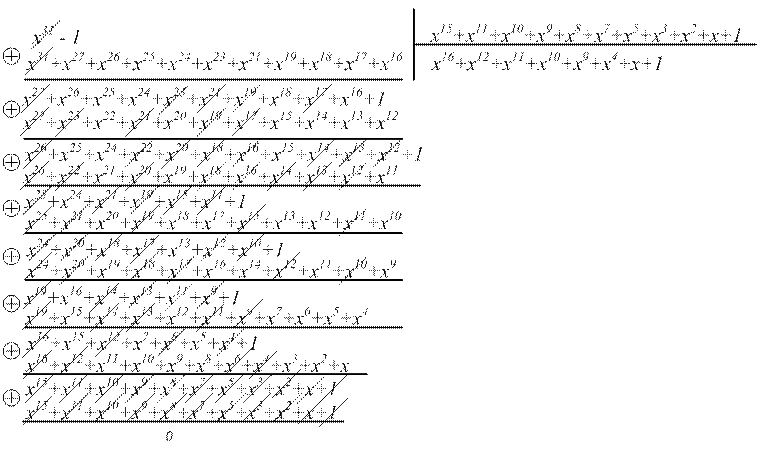
h(x) = x16+x12+x11+x10+x9+x4+x+1
σ(x) → 98010 → 11110101002 → x9+x8+x7+x6+x4+x2
R(x) = [σ(x) * xn-k ] mod p(x) [8]
σ(x) * xn-k = (x9+x8+x7+x6+x4+x2) * x15 = x24+x23+x22+x21+x19+x17
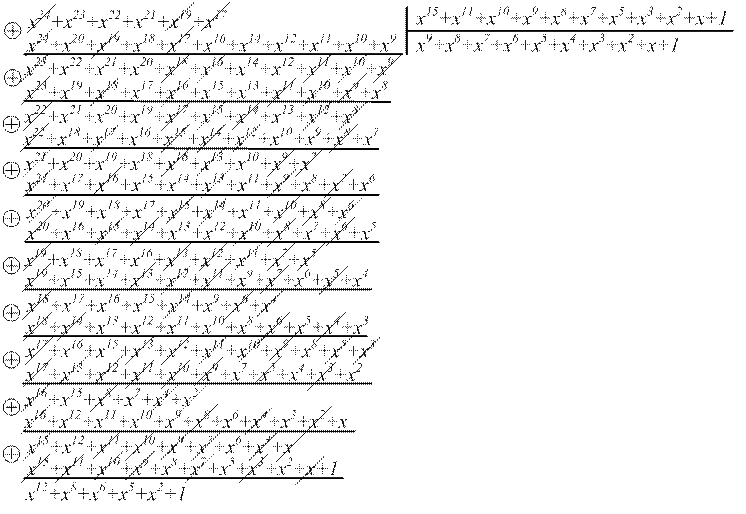
R(x) = x12+x8+x6+x5+x2+1
F(x) = σ(x) * xn-k + R(x) [9]
F(x) = x24+x23+x22+x21+x19+x17 + x12+x8+x6+x5+x2+1
F*(x) = F(x) + E(x) [10]
F*(x) = x24+x23+x22+x21+x19+x17+x12+x8+x6+x5+x2+1 + x21 = x24+x23+x22+x19+x17+x12+x8+x6+x5+x2+1
Sне сел. = E(x) / p(x) [11]
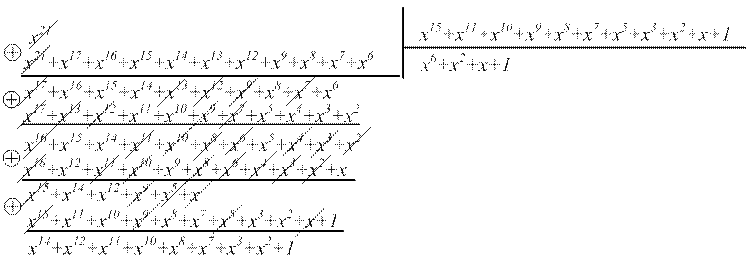
Sне сел. = x21/ x15+x11+x10+x9+x8+x7+x5+x3+x2+x+1 = x14+x12+x11+x10+x8+x7+x3+x2+1
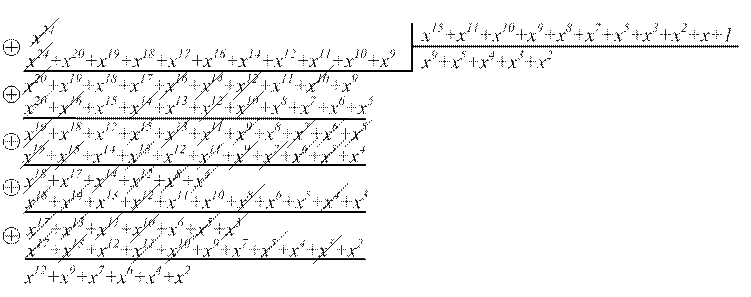
Sсел. = x24/ x15+x11+x10+x9+x8+x7+x5+x3+x2+x+1 = x12+x9+x7+x6+x4+x2
Список литературы:
1. Кодировние сообщений: метод. ук. к лаб. раб./ А.Б. Жуков, С.В. Каменский – Новосибирск: НГТУ, 2003.-60с. №2495 004 К577
[1] стр.5
[2] стр.7
[3] стр.7
[4] стр. 35
[7] стр.49
[8] стр.50
[9] стр.50
[10] стр.51
[11] стр. 51
2. Тутевич В.Н. Телемеханика.-М.: Высш.шк. 1989г.
[5] стр.83
[6] стр.87
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.