Закон электромагнитной индукции. Закон полного тока, страница 2

          В этом случае ЭДС е, индуктируемая в обмотке, также будет изменяться по синусоидальному закону и достигнет максимума при наибольшей скорости изменения магнитного потока, т. е. в момент перехода потока через нуль. При максимальном значении потока скорость его изменения равна нулю и е = 0. Изменение ЭДС имеет характер, изображенный на рис. 1.3, б, и описывается формулой

                                                                                    (7)

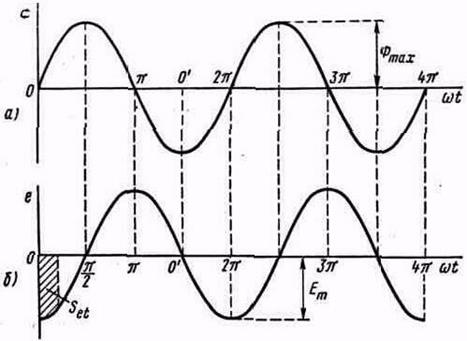
Рис. 3

Величину Е_m можно определить, исходя из следующих соображений.

Учитывая, что в данном случае

,

и используя формулы (5) и (7), получим соотношение между амплитудными значениями магнитного потока (или индукции) и ЭДС:

                                                                          (8)

Практически наиболее часто к зажимам обмотки, расположенной на сердечнике, подключается синусоидальное напряжение источника питания (рис. 3, а)

                                                    (9)

Для электрической цепи, образуемой обмоткой сердечника, справедливо уравнение

                                             (10)

где R - активное сопротивление обмотки; U_L - мгновенное значение части напряжения на индуктивной составляющей цепи.

В большинстве случаев можно принять, что iR << U_L. Тогда

                                                    (11)

Если воспользуемся формулой (5), то получим закон изменения потока в сердечнике (рис. 4, б).

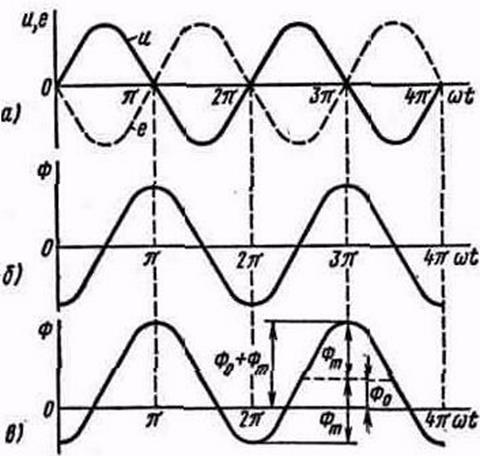
Рис. 4

Из рис. 4, а, б видно, что изменение магнитного потока отстает на угол  p/2 от изменения напряжения сети и определяется выражением

                                                                         (12)

Так как Еm =Um, то амплитудное значение магнитного потока находим, используя формулу (8):

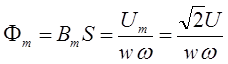                                                               (13)

или

                                                                    (14)

где U-действующее значение переменного напряжения; f=w/2p-его циклическая частота.

Таким образом, если можно пренебречь падением напряжения на активном сопротивлении iR в обмотке сердечника, то можно считать, что приложенное к обмотке синусоидальное напряжение вызывает синусоидальное изменение магнитного потока, амплитудное значение Фm, которого не зависит от магнитных характеристик и геометрических размеров сердечника.

Иногда в сердечнике наряду с переменной составляющей потока имеется также постоянная составляющая Фo, обусловленная, например, наличием постоянного тока в обмотке сердечника. Однако если можно пренебречь падением напряжения на активном сопротивлении iR, то наличие постоянной составляющей потока Фo не может повлиять на закон изменения переменной составляющей потока или на ее амплитудное значение Фm. Поэтому в общем случае магнитный поток в сердечнике при синусоидальном напряжении на зажимах его обмотки определяется формулой

                                                                            (15)

где Фm вычисляется по формуле (13).

На рис. 4, в показано изменение магнитного потока при наличии постоянной составляющей Фо и синусоидальном напряжении, изображенном на рис. 1.4, а.

Закон полного тока

Намагничивающая сила, действующая в сердечнике

                                                                    (16)

где iw - сумма токов, протекающих через окно сердечника.

Намагничивающая сила, приходящаяся на единицу длины сердечника, равна напряженности магнитного поля Н.

Предположим, что намагничивающая сила распределена равномерно по всей длине сердечника, что имеет место лишь у сердечников с одинаковыми по длине магнитными свойствами и поперечным сечением. Тогда согласно закону полного тока среднее значение напряженности поля сердечника равно намагничивающей силе, действующей вдоль замкнутого контура, т. е. сумме всех токов, пронизывающих этот контур

                                                                  (17)

где l - средняя длина сердечника (длина средней силовой линии).

Таким образом, напряженность магнитного поля в однородном сердечнике однозначно определяется токами в его обмотках. Если известны величина и характер изменения напряженности поля, то по формуле (17) можно вычислить и ток в его обмотке. Если на сердечнике имеется несколько обмоток w1,w2,w3,…,wn , пo которым протекают соответственно токи i1 ,i2 , i3 ,…, in то результирующая напряженность поля

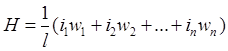                                           (18)