Закон электромагнитной индукции
Процессы, происходящие в магнитном материале, характеризуются магнитными величинами: магнитной индукцией В или магнитным потоком Ф и напряженностью магнитного поля Н. Процессы в электрических цепях, в том числе и в цепях, содержа щих магнитный сердечник, характеризуются электрическими величинами: током i, напряжением U и электродвижущей силой e. Между указанными магнитными и электрическими величинами существует связь, которая устанавливается на основе закона электромагнитной индукции (закона Фарадея) и закона полного тока. При анализе процессов в электрических цепях с магнитными сердечниками существенную роль играет также закон непрерывности магнитного потока.
Рассмотрим кольцевой сердечник, изображенный на рис.1. Если под действием тока i, протекающего по его обмотке, в магнитном материале установится некоторая индукция В, то магнитный поток, проходящий через площадь поперечного сечения S сердечника,
·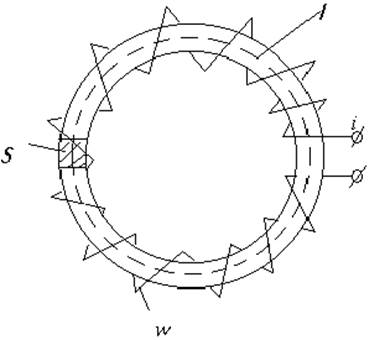
Рис. 1
Ф=ВS. (1)
Согласно закону электромагнитной индукции при всяком изменении магнитного потока Ф сердечника в его обмотке индуктируется ЭДС е, величина которой прямо пропорциональна скорости изменения потокосцепления Y, т. е. скорости изменения магнитного потока и числу витков обмотки w
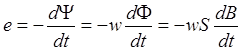 (2)
(2)
Если замкнуть концы обмотки w, то в ней под действием индуктируемой ЭДС потечет ток i в таком направлении, при котором его магнитное поле будет противодействовать изменению магнитного потока Ф. Это правило, открытое Ленцем, объясняет знак минус в формуле (1).
·Задача 1.1.
А. Определить, как изменяется ЭДС, наводимая в обмотке сердечника, при условии изменения магнитного потока в сердечнике по трапецеидальному закону (рис. 2.,а).
·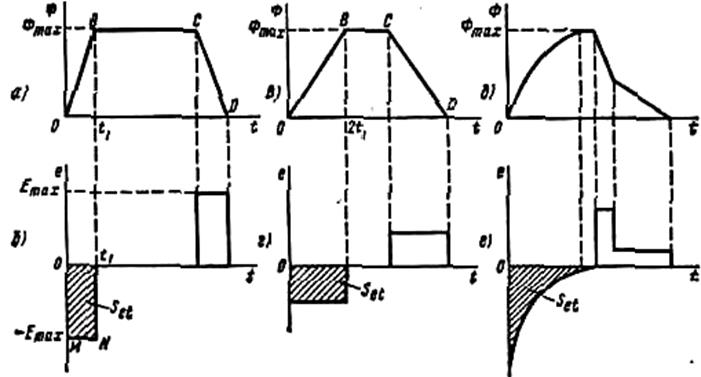
Рис. 2.
Решение. На участке 0В поток изменяется с постоянной скоростью до значения Фmax. При этом
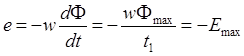
На участке ВС поток не изменяется и
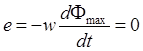
На участке CD поток убывает с постоянной скоростью.
Изменение ЭДС показано на рис. 2.,6.
Б. Определить, как изменится ЭДС при изменении магнитного потока по трапецеидальному закону до того же значения, что и в предыдущем случае, но с вдвое меньшей скоростью (рис. 2., в).
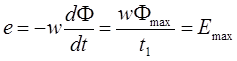
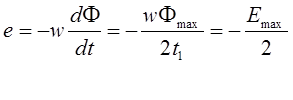
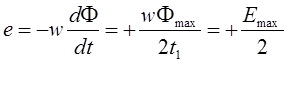
На участке ВС е = 0.
Таким образом, амплитуда ЭДС, индуцируемой в обмотке w, уменьшается вдвое, а длительность импульса ЭДС вдвое повышается, так как для достижения заданного максимального значения Фmax требуется в два раза больше времени, чем в предыдущем случае. На рис. 2, д показано изменение потока от 0 до Фmax по произвольному закону, а на рис. 2, е изображена кривая ЭДС, которая индуктируется при этом в обмотке. Площадь, образуемая кривой ЭДС с осью времени, в этом случае равна площади отрицательного импульса напряжения (OMNt1 на рис. 2., б)
Из рис. 2, а - г, показывающих изменение магнитного потока в сердечнике и соответствующие изменения наводимой ЭДС в обмотке, очевидно, что площадь, образуемая импульсом ЭДС с осью времени, зависит не от скорости изменения магнитного потока, а только от начального и конечного значений магнитного потока. Эта площадь (на рис. 2, б, г, е заштрихована) не зависит также и от закона изменения магнитного потока.
Если обозначить эту площадь через Set, то связь, которая существует между этой площадью и конечным изменением магнитного потока DФ (на рис. 2 DФ = Фmax - 0), для всех магнитных сердечников и магнитных материалов при любом законе изменения магнитного потока определяется формулой
![]() (3)
(3)
Площадь Set часто называют вольт-секундной площадью. Кроме того, величину вольт-секундной площади можно определить как
![]() (4)
(4)
В этом случае формула (3) может быть записана в виде
![]() или
или
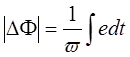 (5)
(5)
Таким образом, зная величину наведенной ЭДС (вольт-секундную площадь) и число витков обмотки, однозначно можно определить величину изменения потока в сердечнике.
Немаловажное значение имеет случай, когда магнитный поток в сердечнике изменяется по синусоидальному закону (рис.3, а):
![]() (6)
(6)
где w- угловая частота; Фm и Вm - соответственно амплитудные значения магнитного потока и магнитной индукции.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.