Зависимость характеристик сердечников от их геометрической формы и воздушных включений

ЗАВИСИМОСТЬ ХАРАКТЕРИСТИК СЕРДЕЧНИКОВ ОТ ИХ ГЕОМЕТРИЧЕСКОЙ ФОРМЫ И ВОЗДУШНЫХ ВКЛЮЧЕНИЙ

Длина магнитного пути по наружному и внутреннему периметрам кольцевого сердечника неодинакова. Поэтому напряженность поля, обусловленная током в обмотке, различна по сечению сердечника. Это вызывает существенное изменение вида статической петли гистерезиса кольцевого сердечника с прямоугольной петлей (ППГ). Пониманию вопроса способствует рис.1. Сердечник изготовлен из однородного магнитного материала с идеальной ППГ и пронизывается проводом с током .Если представить, что сердечник стоит из большого числа очень тонких цилиндрических слоев толщиной  и каждый такой слой характеризуется свойствами материала, т. е. имеет идеальную петлю гистерезиса(рис.2, а), то можно показать, что ста­тическая петля гистерезиса такого сердечника будет иметь вид па­раллелограмма согласно (рис. 2, б).

Это обусловлено следующими причинами. Пусть  - напряженность магнитного поля в слое;  - магнитная индукция слоя,  - максимальная магнитная индукция слоя; ,  — соответствен­но, средняя и максимальная индукции сердечника.

Тогда

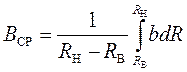 .                                                   (1)

Так как в различных слоях сердечника напряженность поля не­одинакова, то за среднее значение напряженности поля в сердеч­нике можно взять такое, которое имеет слой, находящийся от оси от провода на расстоянии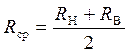

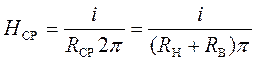                                         (2)

Цилиндрический слой , расположенный на расстоянии , может перемагнититься только в том случае, если напряженность поля в нем достигнет

величины . Расстояние , учитывая (2),можно определить как

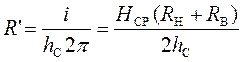 .                                                               (3)

Слои, находящиеся в пределах , будут перемагниче­ны в состояние, соответствующее  (если перед действием тока все слои сердечника были в состоянии ), а слои, находящиеся в пределах , останутся в состоянии . Согласно это­му уравнение (1) можно переписать в виде

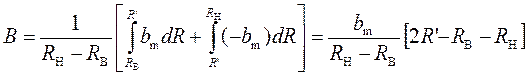  .         (4)

 Если все слои сердечника обладают однородными свойствами, то , и тогда, подставляя выражение (3) в (4), имеем

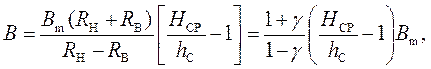                                   (5)

где 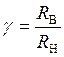 — отношение радиусов сердечника.

Если , то из (5) имеем , но для сердечника вели­чина при  есть коэрцитивная сила ; значит, . По­этому уравнение (5) можно записать в виде

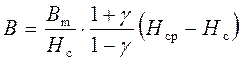 .                                                                        (6)

Величина

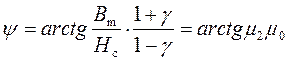                                                             (7)

характеризует угол наклона восходящей (тоже можно получить и для нисходящей) петли гистерезиса. Из выражения (7) видно, что наклоны боковыхсторон петли гистерезиса зависят от отношения радиусов сердечника. При все более тонкой стенке сердечникаугол  приближается к 90°, т. е. такой сердечник будет иметь идеальную прямоугольную петлю гистерезиса с проницае­мостью на восходящей ветви .

Величины  и  (рис. 2, б) представляют собой те значения напряженности поля, действующей по средней линии сердечника, при которых соответственно начинается и кончается процесс перемагничивания сердечника. Из выражения (3) при  и  получим, считая ,

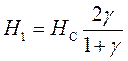 ;                                                                 (8)

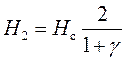  .                                                                 (9)

Проведенный приближенный анализ позволяет сделать вывод о том, что отношение внутреннего и внешнего диаметра существен­но влияет на магнитные свойства сердечника с ППГ.

Пример. Пусть два сердечника с ППГ размерами  мм и  мм выполнены из одного материала, имеющего идеальную прямо­угольную петлю гистерезиса, с параметрами  Т,  А/м. Определим, какой из двух сердечников имеет большую величину проницаемости  на восходящем участке петли гистерезиса.

Для первого сердечника ; для второго .Соглас­но (7) имеем :