Классификация протоколов удаленного взаимодействия абонентов. Протоколы контроля целостности информации. Протоколы идентификации и аутентификации абонентов в сети, страница 9

S_m – двоичный вектор с размерностью m

S1,S2,S3…Sn – векторы

 S1S2S3…Sn

P_под=2^-m

Достоинства:

Простота реализации

Недостаток:

Для восстановления ключа необходимо наличие всех пользователей из заданной группы

Пороговая схема разделения секретов на основе многочленов Лагранжа

t – подгруппа из t-пользователей

1<t<=n

Задача: Построить схему разделения секрета между n-пользователями, в которой любая группа из t-пользователей может восстановить секрет. При этом никакая группа из меньшего количества пользователей не может восстановить секрет.

(n,t) – пороговая схема

Формирование долей секрета:

1)  Выбирается конечное поле GF (P)

Генерируется r-несекретные элементы
r1,r2,r3,..,rn GF (P)

ЦРКàAi:ri

2)  Выбирается t+1 случайных элементов a0,a1,a2…,at  GF (P)
Данные элементы являются коэффициентами формального многочлена над конечным полем степени t

f(x)=

3)  Задается значение секрета в точке x=0
S=f(0)=a₀

Далее определяются доли секрета S2=f(r2),…,Sn=f(rn)
ЦРКàAi:Si
Ai: (ri:Si)

Восстановление секрета

Используется многочлен Лагранжа в следующем виде:

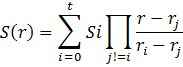
 mod p

Пример:

n=6	r1=1
t=3	r2=3
a0=2	r3=5
a1=3	r4=7
a2=1	r5=4
	r6=2

f(x)=2+3x+x²mod 11

S=2

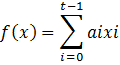
S1=10

S2=7

S3=

S4

S5

S6=0

S=6*(3/(3-1))*(2/(2-1))+9*(1/(1-3))*(2/(2-3))+1*(1/(1-2))*(3/(3-2)) mod 11

S=18+9-3=24mod11=2

Особенность:

На практике значение характеристики поля, т.е. значение P должно быть больше 2⁵¹²

Данная схема позволяет легко увеличивать число пользователей (n,t)à(n+k,t)

В случае компрометации одной из долей секрета проходим в (n-1,t-1)

Достоинство данной схемы:

Возможность восстановления секрета заданной группы пользователей из всего множества пользователей.

Схема установления ключей для конференцсвязи

Основное отличие схемы установления ключа для конференцсвязи от обмена секретом в том что ключ вырабатывают в процессе обмена информации, а не распространяют доли известного ключа.

Для установления ключа используется открытое распределения ключей на основе схемы Дифа-Хелмана

Большое простое число P>2⁵¹²

α - примитивный элемент Zp

А,В,С - пользователи

Каждый из этих пользователей генерирует свой секретный ключ

1)  A:x, B:y, C:z

Секретные ключи: x,y,zZp

2)  AàB: X=α^xmodp

3)  BàC: Y=α^ymodp

4)  CàA: Z=α^zmodp

5)  AàB: Z’=Z^xmodp

6)  BàC: X’=X^ymodp

7)  CàA:Y’=Y^zmodp

8)  Каждый из пользователей генерирует общий секретный ключ
A:K=Y’^xmod p = Y^zxmodp=α^yzxmodp
B:K=Y’^ymod p = Y^xymodp=α^zxymodp

С:K=Y’^яmod p = X^yzmodp=α^xyzmodp

Для задачи аутентификации необходимо применять электронно-цифровую подпись

Вместо классической схемы Дифа-Хелмана может применятся способ эллиптических кривых, при том в сети будет передано n*(n-1) сообщение.

Стандарт эллиптических кривых

Современный стандарт ЭЦП

Тенденция развития ЭЦП:

Российский стандарт ГОСТ Р 34.10-2001

Сравнение систем ЭЦП и атаки на ЭЦП

[Электронная] цифровая подпись (digital signature): Строка бит, полученная в результате процесса формирования подписи. Данная строка может иметь внутреннюю структуру, зависящую от конкретного механизма формирования подписи.

Области применения ЭЦП

Придание электронному документу юридического значимого статуса:

·  электронное правительство

·  электронная коммерция

·  электронный документооборот

·  электронные платежи

Обеспечение ИБ

·  система доступа к ограниченным информационным системам и ресурсам

·  аутентификация пользователей

·  обеспечение целостности информации

Законы и решения Правительства

·  Закон «Об электронной цифровой подписи»

·  Закон «Об электронном документообороте»

·  Закон «Об электронной коммерции»

Постановление Кабинета Министров от 26.09.2005 №215:

·  Положение о государственной регистрации центров регистрации ключей ЭЦП

·  Положение о деятельности центров регистрации ключей ЭЦП

Качества ЭЦП

1)  Подпись достоверна. Она убеждает получателя в том, что подписавший сознательно подписал документ.

2)  Подпись неподдельна. Она доказывает, что именно подписавший сознательно подписал документ.