Расчет дощатоклееной армированной балки с двойным армированием. Статический расчет шарнирной рамы, страница 2

Наименование нагрузки	Нормативная величина нагрузки	gf	Расчетная величина нагрузки
1. Постоянная от собственного веса гравий втопленный в битумную мастику (20мм) стеклорубероид (3 слоя) фанерных обшивок утеплитель из минваты толщиной 200 мм и плотностью 75 кг/м3 продольных ребер поперечных ребер 20% приборов освещения (5 кг/м2)	0,2 0,1 0,16 0,15 0,15 0,03 0,05	1,2 1,2 1,1 1,2 1,1 1,1 1,2	0,24 0,12 0,18 0,18 0,17 0,03 0,06
Итого постоянная	0,84		0,98
2. Снеговая для г. Тамбов (III р-н)	1,0	1,6	1,6

Расчетные усилия в панели:

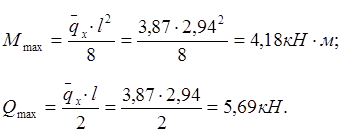
Геометрические характеристики приведенного сечения панели.

Коэффициент приведения для древесины:

Высота панели , что составляет:  пролёта.

Приведенная площадь сечения:

Приведенный статический момент сечения относительно нижней его грани:

Координаты нейтральной оси приведенного сечения:

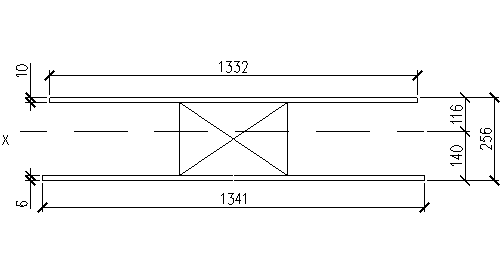
Рис.3 Конструкция коробчатой клеефанерной кровельной панели размером 1,5 х 3 м (расчетное сечение).

Приведенный момент инерции (без учёта собственных моментов инерции обшивок):

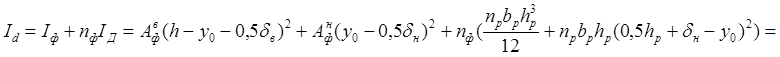
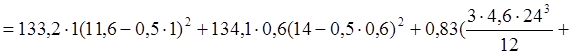
Приведенные моменты сопротивления:

Проверка прочности верхней обшивки на местный изгиб:

Проверка устойчивости сжатой обшивки:

Проверка прочности на скалывание по клеевому шву:

где

Проверка жесткости при Е_p=12000 МПа (см. табл. 6.12 СНБ5.05.01-2000):

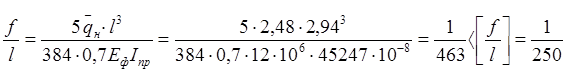
Приведенный расход древесины:

Сравнение 2-х вариантов

принимаем клеефанерную панель покрытия заводского изготовления.

2 Расчет дощатоклееной армированной

балки с двойным армированием.

Исходные данные для расчета: пролет балки по осям 21м; уклон кровли 0,05; шаг балок 3м; район строительства – г. Тамбов; материал конструкций – кедр второго сорта; доски 200x50мм в заготовке.

Для приближенного определения нагрузки от собственно массы балки можно воспользоваться формулой:

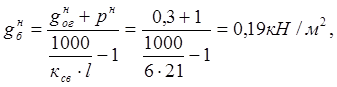
где   коэффициент нагрузки от собственной массы;

 расчетный пролет конструкции.

 снеговая нагрузка для горизонтальной проекции;

нормативная           

расчетная                       

Полная погонная нагрузка на балку:

нормативная    

расчетная

Приняв предварительно (табл. 6.8 [1]) и (табл. 6.7 [1]) при высоте балки   вычислим расчетные сопротивления древесины балки:       

Найдем наибольший изгибающий момент:

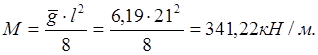
Наибольшая поперечная сила:

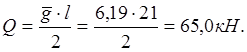
Требуемый момент сопротивления:

где   коэффициент армирования, принимаем ;

 коэффициент приведения арматуры к древесине, примем .

Ширина сечения балки после фрезерования может быть принята равной . Тогда требуемая высота балки будет определяться:

из условия прочности ее на изгиб

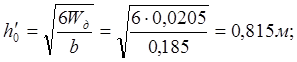
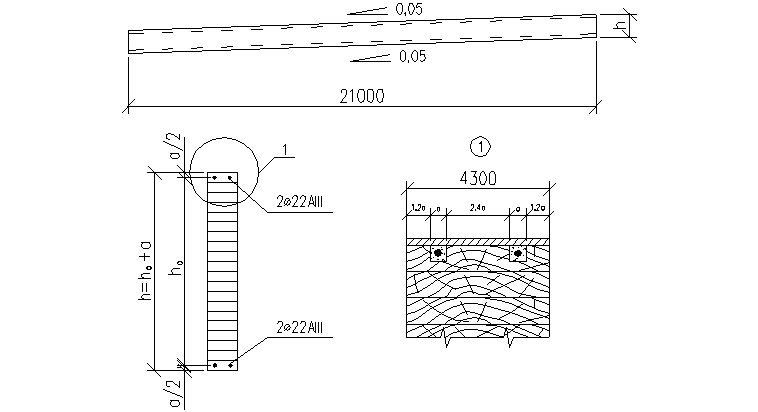
Рис.4 Конструктивная сема балки, сечение балки.

из условия прочности на скалывание

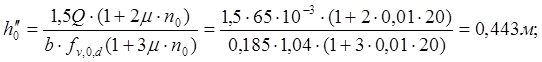
Из условия жесткости требуемый момент инерции приведенного и деревянного сечений:

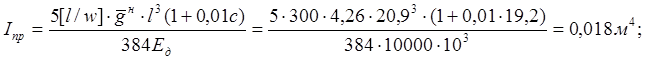
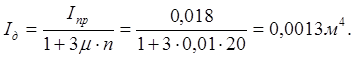
требуемая рабочая высота балки из условия жесткости:

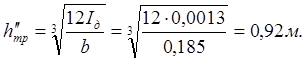
Высота балки  Окончательно принимаем высоту балки . Тогда рабочая высота балки .

Выполняем проверочные расчеты принятого сечения балки.

Коэффициент армирования:

Приведенный момент инерции сечения:

Приведенный момент сопротивления: