Решение уравнения методом касательных

            Министерство Образования Республики Беларусь

              Гомельский Государственный Технический

                      Университет им П.О. Сухого

              Кафедра:”Информационные технологии.”

                         Курсовая работа на тему:

            “Решение уравнения методом касательных.”

                                                 Выполнил студент гр ТЭ-22

                                                        Кортелев Д .Н.

                                                  Принял преподаватель

                                                             Косинов Г.П.          

                                  Гомель.   

Содержание

          Введение

1.  Постановка задачи…………………………………………………..

2.  Теоретические сведения о процедурах и функциях………………………..………..…………………………..

3.  СистемЄое и техническое обеспечение…………………………….

4.  Исходные данные……………………………………………………

5.  Моделирование работы пользователя с программой……………..

6.  Структура программного комплекса……………………………….

7.  Разработка структуры данных……………………………………...

8.  Составление алгоритма программы………………………………...

9.  Составление программы……………………………………………..

10.Подготовка тестов для последующей отладки программы……….

11. Отладка программы………………………………………………….

12.Построение графиков в пакете Mathcad и их анализ..………….….

Заключение…………………………………………………………

Литература………………………………………………………….

Приложение 1………………………………………………………

Приложение 2………………………………………………………

Приложение 3………………………………………………………

Введение

          В решении актуальных задач ускорения научно-технического прогресса существенная роль принадлежит ПЭВМ.

          Высокая производительность, малые габариты и энергопотребление, развитое, ориентированное на массового пользователя базовое и прикладное ПО, обеспечивают значительное повышение эффективности труда в различных отраслях народного хозяйства.

          Широкое применение ЭВМ в технологической подготовке производства требует от инженерно-технических работников знания вопросов автоматизации инженерного труда. В полной мере это относится и к специалистам, занимающимся вопросами инструментального проектирования.

          В связи с широким использованием ЭВМ в различных сферах инженерного труда изменился и сам характер процесса проектирования. Создание и использование систем автоматизированного проектирования (САПР) позволяет уменьшить трудоемкость процесса проектирования, в 10-50 раз сократить сроки его выполнения, качественно изменить труд конструктора. Применение ЭВМ ликвидирует рутинные, нетворческие этапы проектирования, но при этом усиливаются значение неформальных элементов – оценки результатов, принятие решений и др.

Целью данной курсовой работы является создание программы, автоматизирующую расчет решения уравнения численным методом.

1.  Постановка задачи.

Требуется решить уравнение вида:

методом уточнения корня: касательных, при точности 0,0001.

Пусть функция f(x) имеет корень (нуль) в промежутке [a, b]. Будем предполагать, что f имеет производные первого и второго порядков и f’(x) ¹ 0 на [a, b], т.е. f(x) монотонна на этом сегменте. Это говорит о том, что на [a, b] имеется хотя бы один корень функции f.

Составим вспомагательную функцию

             F(x) = x + k(x)*f(x),

Где k(x) – некоторая непрерывно дифференцируемая функция, не равная нулю. Ясно, что неподвижная точка x функции F является нулем f и обратно.

Поэтому, если функция F отображает [a, b] в [a, b] и является сжимающей на [a, b], то итерационная последовательность x_n = F(x_n-1) сходится к неподвижной точке F ( т.е. корню f), а x_n можно взять за приближенное значение корня. При различных k(x) мы получим различные приближенные методы вычисления корня функции f(x).

          Приближенный метод вычисления корня функции f(x) (x_n » x) при       k(x) = -1/f’(x) носит название метода Ньютона или метода касательных. Элементы итерационной последовательности { x_n } можно получить из геометрических соображений.

          Если x_n-1 Î [a, b] уже определено, то для получения x_n в точке (x_n-1 , f(x_n-1)) графика функции f проводим касательную. Точку пересечения этой касательной с осью х берем за x_n . Уравнение касательной имеет вид:

          Y - f(x_n-1) = f’(x_n-1)(x - x_n-1).

          Полагая в этом равенстве Y = 0, найдем решение x = x_n , где   

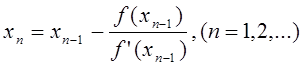          Таким образом, числа x_n являются элементами итерационной последовательноси для функции:

 

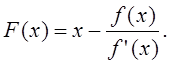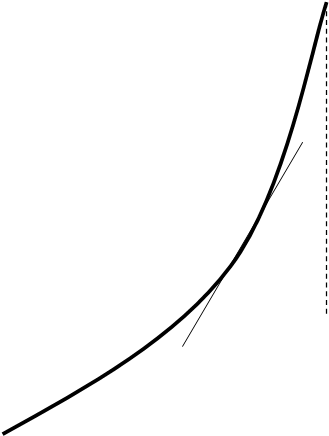                                                                       (x_n-1 , f(x_n-1))

 

             0                     a                                    x_n  x_n-1         b

2. Краткие теоретические сведения о процедурах и функциях.

          Процедура предназначена для выполнения какой-то законченной последовательности действий. Любая процедура начинается с заголовка. В отличие от основной программы заголовок в процедуре обязателен. Он состоит из зарезервированного слова procedure, за которым следует идентификатор имени процедуры, а далее в круглых скобках – список формальных параметров:

procedure <имя процедуры>(< список формальных параметров >);

<раздел описаний>

begin

  <раздел операторов>

end;

          За заголовком могут идти такие же разделы, что и а основной программе