|
Нгрузки |
Нагрузки, кПа |
||
|
норм-е |
γf |
расч-е |
|
|
Постоянные |
|||
|
1.Пол |
3 |
1,2 |
3,6 |
|
2.Плита перекрытия |
12 |
1,15 |
13,8 |
|
3.Ригель(b=0,25м;h=0,6м) |
3,75 |
1,1 |
4,125 |
|
Итого |
18,75 |
21,525 |
|
|
Временные |
|||
|
3.Стац-е оборуд. |
24 |
1,2 |
28,8 |
|
4.Вес людей и мат-в. |
60 |
1,3 |
78 |
|
Итого |
84 |
106,8 |
|
|
Суммарные |
|||
|
5.Полные |
102,75 |
128,325 |
|
|
6.В т.ч. длит-е |
42,75 |
50,325 |
|
Изгибающие моменты в пролетном и опорном сечениях определяются по формуле:
![]()
1. М1 = (0,078·21,53 + 0,1·106,8)·4,22 = 218 кН·м;
М2 = (0.033·21,53 – 0.046·106,8)·4,22 = -74 кН·м;
М3 = (0.046·21,53 – 0.086·106,8)·4,22 = 179 кН·м;
- Мв = (0,105·21,53 – 0,053·106,8)·4,22 = 140 кН·м;
- Мс = (0,079·21,53 – 0,04·106,8)·4,22 = 105 кН·м;
2. М1 = (0,078·21,53 - 0,026·106,8)·4,22 = -19 кН·м;
М2 = (0,033·21,53 + 0,079·106,8)·4,22 = 161 кН·м;
М3 = (0,046·21,53 – 0,04·106,8)·4,22 = -58 кН·м;
3. - Мв = (0,105·21,53 + 0,119·106,8)·4,22 = 264кН·м;
- Мс = (0,079·21,53 + 0,022·106,8)·4,22 = 71 кН·м;
- Мd = (0,079·21,53 + 0,044·106,8)·4,22 = 113 кН·м;
- Мe = (0,105·21,53 + 0,051·106,8)·4,22 = 136 кН·м;
4. - Мв = (0,105·21,53 + 0,135·106,8)·4,22 = 106 кН·м;
- Мс = (0,079·21,53 + 0,111·106,8)·4,22 = 239 кН·м;
- Мd = (0,079·21,53 + 0,02·106,8)·4,22 = 68 кН·м;
- Мe = (0,105·21,53 + 0,057·106,8)·4,22 = 147 кН·м;
Результаты расчета сведены в таблицу 3.
Таблица 3. Максимальные изгибающие моменты в ригеле.



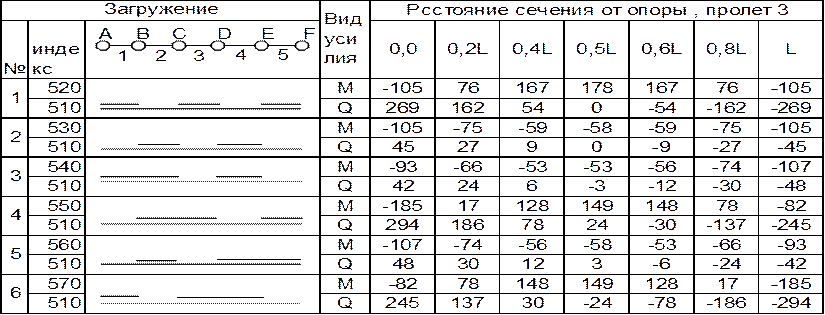
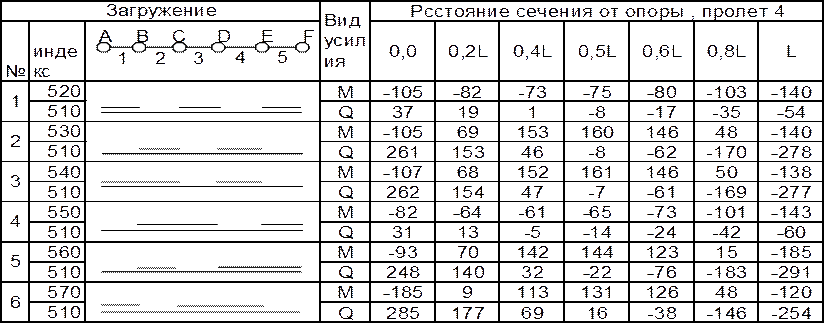

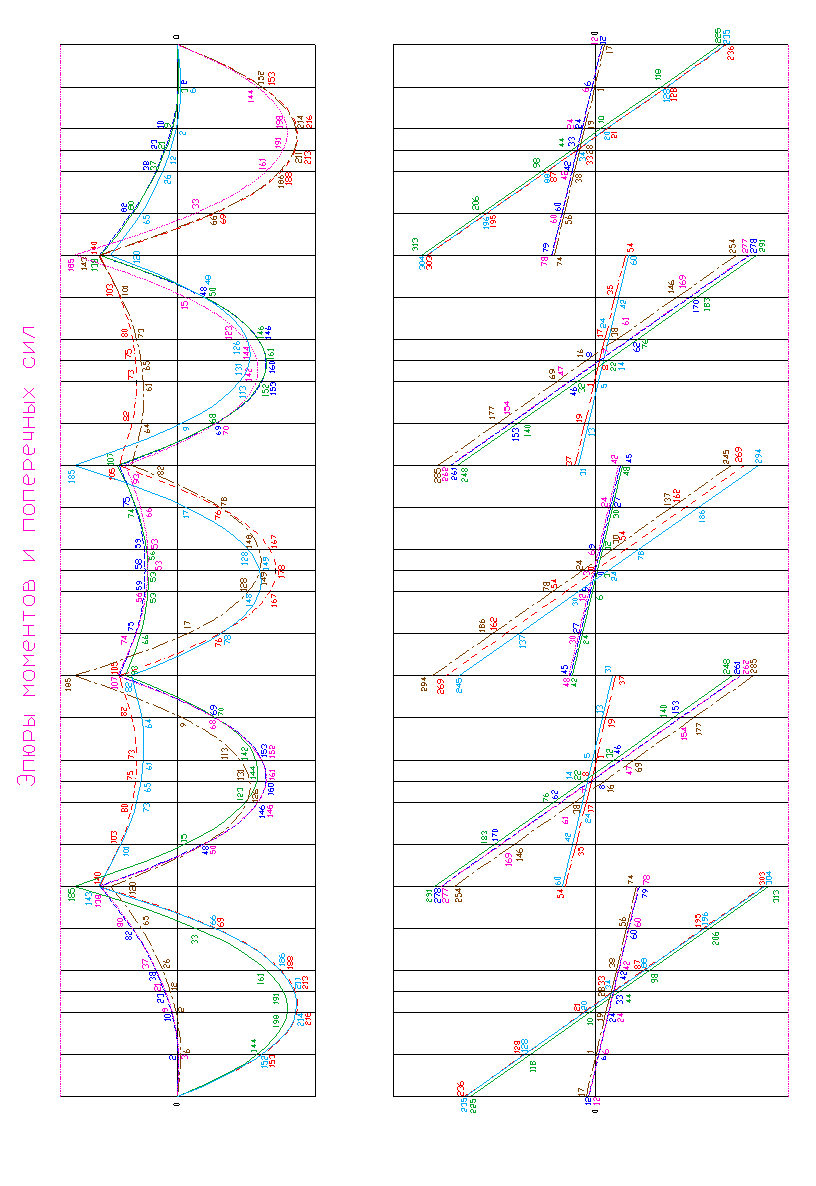 |
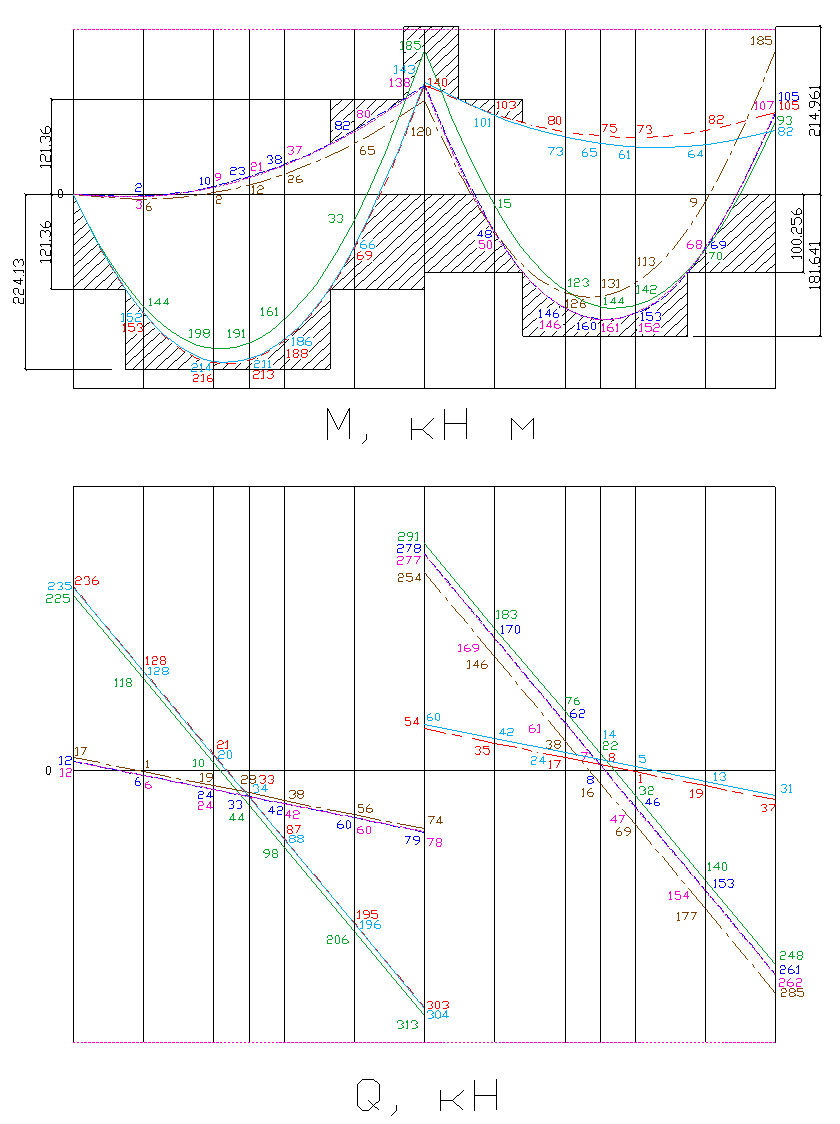
Арматура подбирается для всех пролетов и опор по максимальным пролетным и опорным изгибающим моментам с учетом их перераспределения и симметрии конструкции.
Пролет 1
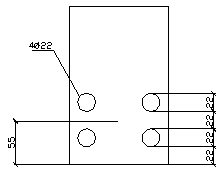
Мsd = 216 кН·м, b × h = 0.25 × 0.6 м, класс бетона С20/25, fcd = 13,3 МПа, класс арматуры S400, fyd = 365 Н/мм2, с = 0,04 м, рабочая высота сечения d = h - c = 0.6 – 0.04 = 0.56 м.
1. Определяем коэффициент αm по формуле:
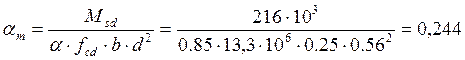
2. Определяем коэффициент ζ по формуле:
![]()
3. Определяем коэффициент ξ lim по формуле:
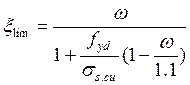
![]()
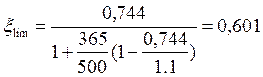
ξ = 0,284 < ξlim = 0,601
4. Определяем требуемую площадь продольной арматуры Аs по формуле:
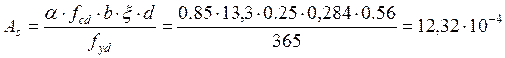 м
м
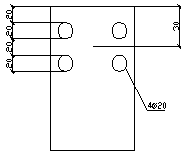
Принимаем 4 стержня диаметром 20 мм с Аs = 12,56 см2.
c = 0.03 м;
d = h – c = 0.6 – 0.03 = 0.57 м
5. ![]()
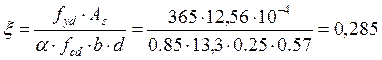
6. ![]()
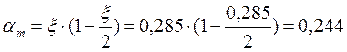
7. Определяем несущую способность сечения при изгибе по формуле:
![]() кН·м
кН·м
MRd = 224,13 кН·м > Msd = 216 кН·м
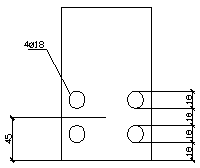 Пролет 2
Пролет 2
Мsd = 161 кН·м,
1. Определяем коэффициент αm по формуле:
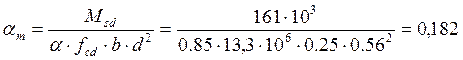
2. Определяем коэффициент ξ по формуле:
![]()
3. Определяем коэффициент ξ lim по формуле:
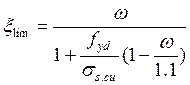
![]()
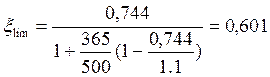
ξ = 0,202 < ξlim = 0.601
4. Определяем требуемую площадь продольной арматуры Аs по формуле:
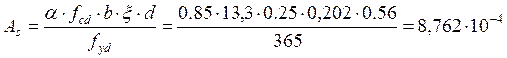 м2
м2
Принимаем 4 стержня диаметром 18 мм с Аs = 10,17см2.
c = 0,045м;
d = h – c = 0.6 – 0,045 = 0,555м
5. ![]()
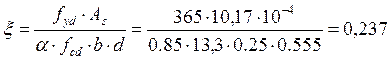
6. ![]()
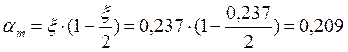
7. Определяем несущую способность сечения при изгибе по формуле:
![]() кН·м
кН·м
MRd = 181,641 кН·м > Msd = 161 кН·м
Опора В
 Мsd = 185 кН·м,
Мsd = 185 кН·м,
1. Определяем коэффициент αm по формуле:
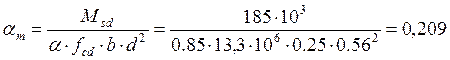
2. Определяем коэффициент ζ по формуле:
![]()
3. Определяем коэффициент ξ lim по формуле:
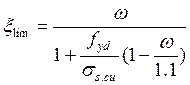
![]()
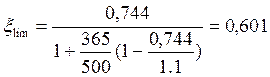
ξ = 0,237 < ξlim = 0.601
4. Определяем требуемую площадь продольной арматуры Аs по формуле:
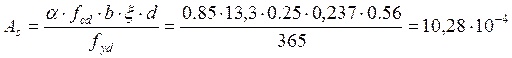 м2
м2
Принимаем 4 стержня Ø 20 мм с Аs = 12,56 см2
5.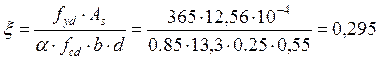
6. 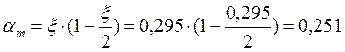
7. ![]() кН·м
кН·м
MRd = 214,961 > Msd = 185 кН·м
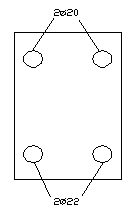 Пролет 1
Пролет 1
Аs = 6,28 см2; А's = 6.28 см2
с = 0,03 м, d = 0,57 м
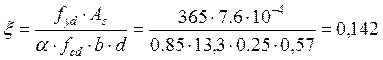
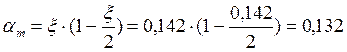
![]() кН·м
кН·м
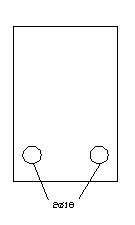 Пролет 2
Пролет 2
Аs = 5,085 см2; А's = 6,28 см2
с = 0,027 м, d = 0,573 м
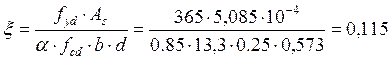
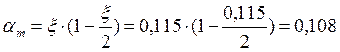
![]() кН·м
кН·м
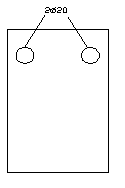 Опора В
Опора В
А's = 6,28 см2
с' = 0,03 м, d = 0,57 м
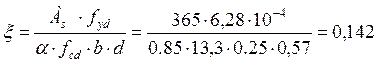
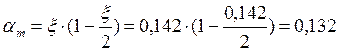
![]() кН·м
кН·м
Пролет 2
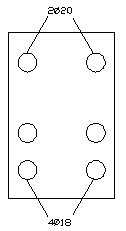 Аs
= 10,17 см2; А's =
6,28 см2
Аs
= 10,17 см2; А's =
6,28 см2
с = 0,045 м, d = 0,555 м
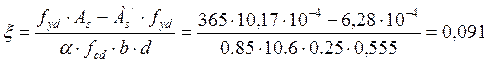
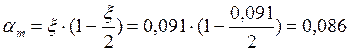
![]() кН·м
кН·м
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.