Математическое программирование: Учебное пособие

видам с учетом имеющихся ресурсов и уста­новленных ограничений, который обеспечивал бы предприятию наивысшую прибыль.

Обозначим через Xjколичество единиц продукции /-го вида, планируемое к выпуску. Тогда суммарная прибыль f{x\, ..., х_п) от реализации выпущенной предприятием продукции при плане про­изводства (х\\...\Хп) определится выражением

f(X_u   ...,  X_n) = (pl-Ci)Xi + ...+ {pn-C„)X_n

или

При этом общий расход £-го ресурса

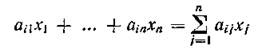
не должен превышать имеющегося запаса Ьи т. е.

Таким образом, ограничения по затратам всех т ресурсов за­пишутся в виде

Ограничения на объемы отдельных видов   выпускаемой   про­дукции выразятся так:

Итак, математически задача сводится к нахождению числовых значений переменных х\, ..., х_п, удовлетворяющих линейным ограни­чениям (1.2), (1.3) и доставляющих максимум линейной функции (1.1). Соотношения (1.1) — (1.3)—математическая модель дан­ной задачи.

Если выпускаемая продукция используется в дальнейшем, то ее, возможно, придется выпускать в определенных пропорциях. В этом случае модель дополняется условиями комплектности. Мо­гут быть и другие ограничения.

В этой задаче мы предполагали все ац и Cjпостоянными вели­чинами, что может не соответствовать действительному положе­нию дел. В реальном производстве не исключается возможность появления брака, доля которого может увеличиваться с ростом ин­тенсивности производства. Предположим, в условиях рассматри­ваемого предприятия установлено, что из-за наличия брака расход ресурсов на изготовление продукции связан с объемом х, ее произ­водства и приближенно выражается функцией

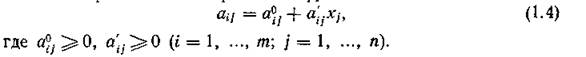
Вместе с этим и себестоимость Cj продукции   зависит   от   объема производства и в первом приближении описывается функцией вида

Подставляя выражения (1.4) и (1.5) в равенства (1.1) и (1.2), по­лучаем

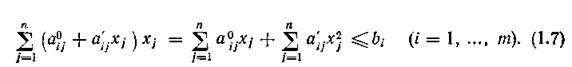
Как видно из соотношений (1.6) и 1.7),  модель  становится  нели­нейной.

Задача об оптимальном составе смеси. Довольно обширный класс задач программирования образуют так называемые задачи на составление смесей или задачи на использование заменителей. Задача подобного рода возникает в случае необходимости смеши­вания различных компонент со сходными свойствами с целью соз­дания смеси, отвечающей определенным требованиям, или при не­обходимости замены в смеси одних компонент другими. Характер­ный пример такой задачи — составление наиболее экономичных смесей горючего' для двигателей разных типов. Известно, что вы­пускаемые марки бензина различаются теплотворной способно­стью, температурой воспламенения, степенью очистки и т. п. Воз­никает задача составления наиболее дешевой смеси из различных марок бензина при условии, чтобы определенные количественные показатели смеси были выше (или ниже) заранее установленных величин. Аналогичной является задача на составление наиболее дешевой смеси различных сортов угля для нагрева паровых кот­лов и т. п.

Не менее важными являются задачи составления экономной шихты для выплавки чугуна и стали. Так, для получения легиро­ванной стали необходимо использовать шихту определенного хи­мического состава. Многие ингредиенты шихты весьма дорогостоя­щие, и вместе с тем в ее состав входят малоценные материалы — чугун, лом, отходы с определенным известным содержанием при­садок. Возникает задача выбора шихты минимальной стоимости, в состав которой должны входить в заданных количествах необхо­димые химические вещества.

К задачам на составление смесей относится также определен­ный тип задач на использование заменителей. Например, проблема замены одних средств производства другими с целью достижения оптимального эффекта производства.

Задачи на смеси приходится решать при определении рацио­нальных норм потребления продуктов питания и в связи с этим при составлении перспективного плана развития пищевой промышлен