Оценка эффективности функционирования сетей связи по частному показателю устойчивости, страница 3

Расчёт вероятностей связности для сложно разветвлённых структур производится различными методами. Исходными данными  для расчётов являются усреднённые прогнозируемые значения вероятностей выживания узлов и линий связи.

Первый метод расчёта вероятностей связности основан на эквивалентном преобразовании сложных (многополюсных) структур к простым двухполюсникам. Под двухполюсной сетью связи (ДСС) понимается часть сети связи, обеспечивающая передачу сообщений между парой абонентов (рис. 2, а).

Под многополюсной сетью связи понимается сеть связи, обеспечивающая одновременную передачу сообщений между двумя и более парами абонентов.

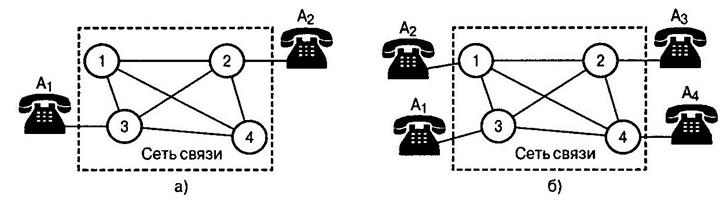
     Рис. 2 Варианты сетей связи: а – двухполюсная, б – многополюсная

Второй метод расчёта вероятности связности сети связи основан на теореме разложения, которая предполагает последовательное разбиение сети относительно выбранных элементов (узлов). При этом процесс разбиения сложно разветвлённой структуры осуществляется до тех пор пока, структура не будет представлена в виде простых параллельно – последовательных соединений.

Теорема разбиения формулируется следующим образом:

• вероятность связности сети связи (Р_св) исследуемой структуры, состоящей из  N  элементов, равна произведению вероятности выживания      i – го элемента на вероятность связности сети связи из (N – 1) элементов при  условии , что i – й элемент замкнут накоротко, плюс произведение вероятности разрушения  i – го элемента на вероятность связности из (N – 1) элементов при условии, что i – й элемент разомкнут.

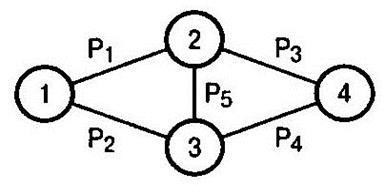
Пример. Задана мостовая структура сети связи (рис. 3), в которой вероятность выживания линий связи Р_выж = 0,36 (за исключением линии между вторым и третьим узлами, которой  Р_выж = 0,85) с требуемой вероятностью связности на направлении от первого до четвёртого узла равной .

                   Рис.3 Вариант мостовой структуры сети связи

Нужно оценить направление связи между первым и вторым узлами сети по структурной живучести. В качестве показателя, характеризующую структурную живучесть направления связи, выбирается вероятность связности. Данная структура разбивается на две аналогичные ей: мостовую схему с замыканием накоротко второго и третьего узлов (рис 4, а) и схему с разрывом линий между ними (рис 4, б). Для каждой модели определяется вероятность связности.

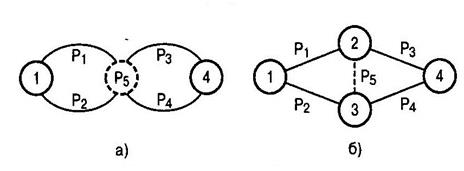
                          Рис. 4 Модели мостовой структуры сети связи

Вероятность связности структуры с учётом параллельной связности элементов сети (рис 4, а):

                                          Р_{св 1} = ,                                                       (14)

где прототип вероятности связности  определяется выражением:

               = [1 – (1 – P₁)·(1 – P₂)]·[1 – (1 – P₃)·(1- P₄)] ≈ 0,35,               (15)

Подставляя значения вероятности прототипа в формулу (14) и учитывая то, что вероятность выживания линии между вторым и третьим узлами составляет Р_выж = Р₅ = 0,85, получаем:

                     Р_{св 1} = 0,35 · 0,85 ≈ 0,35,                                                         (16)

Определим вероятность связности структуры с учётом последовательной связности элементов сети (рис. 4, б):

                        Р_{св 2} = ,                                                                 (17)

Вероятность связности прототипа в этом случае определяется по формуле:

                       = 1 – (1 – Р₁· Р₃) · (1 – Р₂· Р₄) ≈ 0,24                               (18)   

Подставляя найденное значение в формулу (17) получаем вероятность связности направления связи между первым и вторым узлами:

                      Р_{св 2} =  · (1 – Р₅) = 0,24 · (1 – 0,85) ≈ 0,036                      (19)

Для определения вероятности связности направления между первым и четвёртым узлами суммируются значения вероятностей связности для параллельного и последовательного соединений элементов сети связи:

                Р_св = Р_{св 1} +  Р_{св 2}  = 0,3 + 0,036 = 0,336                                       (20)