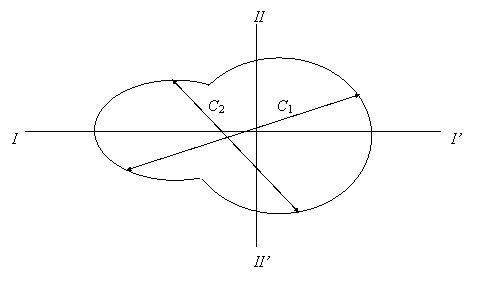
Рисунок 5.1 – Поперечное сечение цилиндрической оболочки конденсатора
Точный расчет
емкости такого конденсатора сопровождается определенными трудностями,
преодолеваемыми путем представления достаточно сложного объекта совокупностью
простых моделей (системы прямых и коаксиальных цилиндров, тороидов, колец с
круглыми или квадратными сечениями, бесконечные плоскости и полуплоскости).
Подробно основы методики воспроизведения емкости с помощью расчетного
конденсатора изложены в [5.3], где показано, что полная “перекрестная”
емкость идеального расчетного конденсатора с длиной цилиндра (электродов) 
равна
,
а ее приращение
.
Из этих формул
видно, что среднее значение удельной емкости 
такого
конденсатора является постоянным. Отклонение от симметрии приводит к поправочным
членам второго порядка малости, столь же мало влияют на параметры
температурного поля. Замечательным свойством конденсатора Томпсона – Лампарда
является то, что для определения емкости требуется только измерение длины , которое можно выполнить с высокой
точностью. Недостаток его – малая емкость (1 пФ на 50 см длины), что требует
построения специальных масштабных преобразователей для передачи размера единицы
в область больших емкостей.
Существует много вариантов конструкции конденсатора с перекрестными емкостями, но оптимальной оказалась конфигурация из четырех параллельных стержней, помещенных в заземленный круговой цилиндр (рис. 5.2) – конденсатор В. Клотье[2] [5.4]. Электрическая и эквивалентная схемы этого конденсатора приведены на рис. 5.3 (а, б).