Общие указания по выполнению контрольной работы по дисциплине "Теоретические основы автоматики и телемеханики", страница 2

Операция «дизъюнкция» (ИЛИ) обозначается символом V (первая буква союза «или то или другое» латинского языка). Условное обозначение элемента, реализующего функцию f=а\/ б, представлено на рисунке  2,б.

Рисунок 2 – Обозначения элементов, реализующих основные

логические функции

Данная функция приобретает значение 1, если хотя бы одно из слагаемых равно 1, т. е. цепь замыкается, когда хотя бы один из контактов замкнут.

Операция «отрицание» (НЕ) обозначается чертой над аргументом. Аргумент   будет равен 0, когда а равно 1, и равен 1, когда а равно 0. Условное обозначение элемента, реализующего функцию отрицания, представлено на рис. 2, в. В контактных схемах операция отрицания, отнесенная к контакту реле, означает замену замыкающего контакта на размыкающий и наоборот.

Введенные символы и логические операции позволяют релейно-контактную схему отобразить структурной формулой.

При выполнении пункта 1, задачи 1 требуется по заданной структурной формуле построить соответствующую ей релейно-контактную схему. В схеме контакты реле включаются последовательно, если они согласно структурной формуле должны выполнять операцию логического умножения, и параллельно - при выполнении операции логического сложения.

В качестве примера рассмотрим следующую структурную формулу:

При наличии отрицания (черты) над суммой или произведением каких-либо двух слагаемых следует преобразовать заданную формулу с учетом соотношений (13) и (14), приведенных ниже.

     Тогда

Релейно-контактная схема, соответствующая рассматриваемой структурной формуле, приведена на рис. 3.

 2. Упрощение (минимизация) структурной формулы. Для упрощения структурных формул необходимо учитывать основные законы и соотношения алгебры логики.

         

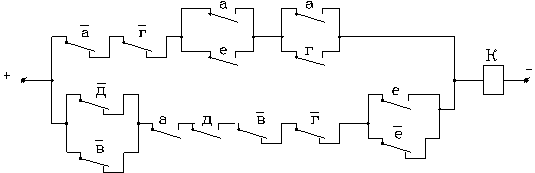
Рисунок  3 – Релейно-контактная схема, соответствующая формуле

  Соотношения, согласующиеся с правилами обычной алгебры:

х \/ 0= х,

x × 0=0;

х · 1=х;

x \/ у = у \/ x,

х · у=у · х;

x × (у · z) = (х × у) × z;

x \/ (у \/ z) = (х \/ у) \/ z,

x (y \/ z) = x × y \/ x × z .

 Соотношения, не имеющие эквивалентов в обычной алгебре:

x \/ 1 = 1 ;                                                 (1)

 x \/ х = х;                                                 (2)

 х · х = х;                                                 (3)

х \/ · (х · у) = х;                                        (4)

 х · (х \/ у) = (х·х) \/ (х · у) =

x \/ (х · у) = x;                                          (5)

  (х \/ у)(х \/ z)=х \/ yz;                              (6)

  (х \/  = 1 ;                                            (7)

 х · = 0;                                                 (8)

  (х \/ у)(х \/ )=х;                                   (9)

  (х · у) \/ (х ·) = х;                                (10)

  (х · ) \/ у = х \/ у;                                (11)

  (х \/ ) у = ху;                                                  (12)

  ()=;                                                 (13)

                                (14)

Различные конъюнкции, входящие в состав формулы, объединяют в группы, содержащие общие элементы, и выносят эти элементы за скобки; указанные операции полезно производить с таким расчетом, чтобы в скобках оставались выражения вида а \/  = 1 либо выражения, к которым могут быть применены различного рода соотношения.     

Члены структурной формулы умножают на единицу, представленную в виде выражения а    , либо прибавляют к формуле функцию вида , равную нулю; указанные операции выполняют так, чтобы в структурной формуле образовать группы, поддающиеся дальнейшему  упрощению.

   К формуле добавляют новые слагаемые из числа тех, которые имеются; затем группируют я выносят общие члены так, чтобы в скобках оставались выражения, равные=1.

    Осуществим упрощение формулы

     

Учитывая, что: 

    а) (а \/ е) (а \/ г) = а \/ ег  (см. соотношение (6) ) ;

    б) е \/  = 1  (см. соотношение (7));

    в)   (см, соотношение (8)),

получим   .

      Структурная формула релейно-контактной схемы имеет вид