Метод диагностирования логических схем, страница 3

 =++ + + + + = =+ + + + .         ₁

За контролирующий тест принимается слагаемое, имеющее наименьшее число цифр, а тест называется минимальным контролирующим тестом

=,

где 3, 5, 6, 7- номера наборов входных переменных.

Обычно контролирующий тест, представляющий собой совокупность наборов, позволяющих проверить исправность устройства, записывается в виде таблицы. Контролирующий тест для логической схемы (рисунок 1) представлен в таблице 3 и выделен прямоугольником.

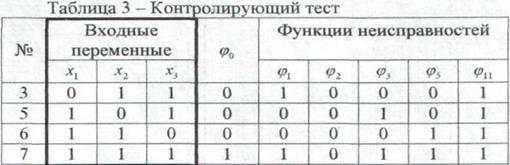
Проверка исправности устройства производится следующим образом: на входы устройства подаются наборы значений сигналов, указанные в контролирующем тесте. Если значения функций на выходе схемы отличаются от значения, то в схеме имеется неисправность.

Для получения диагностического теста, представляющего совокупность наборов входных переменных, позволяющую указать тип и место неисправности, составляется таблица  покрытия  для  пар  функций   (таблица  4).   Столбцы  этой таблицы соответствуют парам различных неисправностей. Заполнение таблицы производится построчным    сравнением    значений    функций    пар    неисправностей. В клетке, соответствующей строке, где значения этих функций не совпадают, проставляются 1.

Таблица 4 - Таблица покрытий функций неисправностей

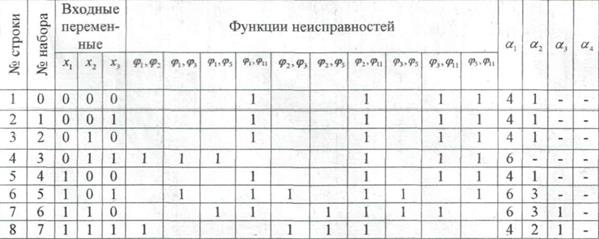
Сравним значения функций неисправностей  и  (смотри таблицу 1). На наборах 3 и 7 значения функций не совпадают. Проставляем единицы в четвертой и восьмой строке первого столбца таблицы 4. Аналогично сравниваем  и т.д. К таблице 4 добавляем несколько столбцов: а₁,а₂,а₃,..., в которых поэтапно отмечаем число единиц в каждой строке. В столбце а₁ проставлено число единиц в каждой строке в начале решения. Далее выбираем одну из строк, содержащую наибольшее число единиц, например, третью строку, где а₁ = 6. В таблице 4 вычеркиваем все столбцы, содержащие 1 в четвертой строке. В столбце а₂ проставляем число единиц в каждой строке, оставшееся после вычеркивания. Снова выбираем строку с наибольшим числом не вычеркнутых единиц. Это строка 6. Вычеркиваем столбцы, содержащие 1 в строке 6. Снова выбираем строку с наибольшим числом не вычеркнутых единиц. Это строка 7. Вычеркиваем столбцы, содержащие 1 в строке 7. Все столбцы вычеркнуты. Таким образом, получена совокупность вычеркнутых строк 4, 6 и 7 (или наборов 3, 5 и 6), составляющая диагностический тест (таблица 5).

.

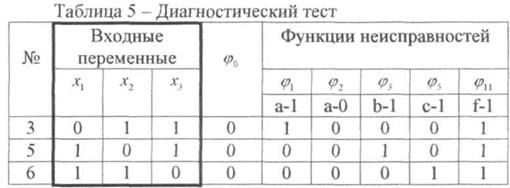
Из таблицы 5 видно, что функции  отличаются друг от друга на наборах 3,5,6 и, следовательно, неисправности, соответствующие этим функциям, можно обнаружить. Обнаружение неисправностей производится следующим образом: на вход устройства подаются наборы сигналов, указанные в диагностическом тесте, и записываются значения функций, получающиеся при этом на выходе схемы. Например, при подаче сигналов набора 3 на выходе получим 1, при подаче сигналов набора 5 на выходе получим 0, а при подаче сигналов набора 6 на выходе получим также 0. По функциям неисправности (таблица 5) видим, что такие значения получаются при неисправности а/1, т.е. неисправность типа 1 в точке а. Если на выходе получили 0 на трех наборах, то в схеме неисправность а/0, и т.д., т.е. неисправности обнаружены.

2 Метод булевой производной (БП)

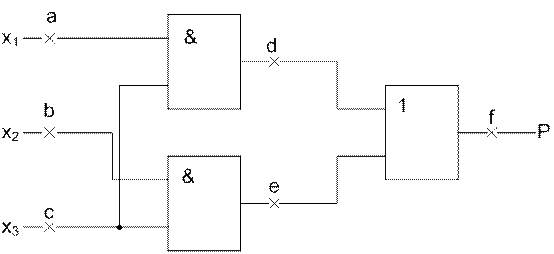
Рисунок 2 – Исследуемая логическая схема

Булевой производной функции f(х) = f(х₁,х₂,...,х_п) по х_i называется функция

где  - сумма по модулю 2.

Булева производная определяет значения логических переменных х_i,...,х_n, кроме х_i, при которых изменение состояния х_i приводит к изменению значения функции f(х). Для нахождения тестовых наборов неисправности х_i/0 (х_i/1) используются выражения вида

Аналогичным образом можно найти и тест-наборы для нахождения неисправности для внутренних переменных схемы. Если значения внутренних переменных у_iподставить в формулу (1) вместо х_i, то можно найти тестовые наборы и для диагностирования неисправности внутри соединительных линий схемы.

Рассмотрим заданную схему (рисунок 2), реализующую функцию

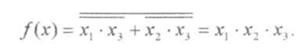
Таблица 6 – Тестирование методом БП

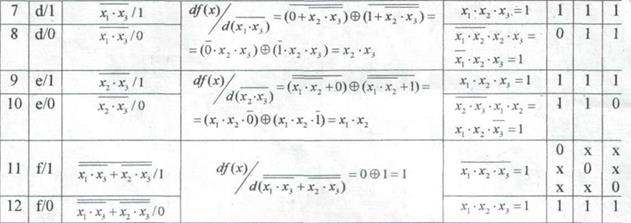
По таблице 6 можно определить тест-наборы для всех неисправностей исследуемой логической схемы. Видно, что тест-наборы некоторых неисправностей совпадают (например 1, 8 или 2, 4, 6, 7, 9, 12), т.е. один тестовый набор контролирует сразу несколько неисправностей.

3 Метод эквивалентной нормальной функции (ЭНФ)

Рисунок 3 – Исследуемая логическая схема