Построение переходных и частотных характеристик линейных САУ: Методическое пособие для подготовки и выполнения лабораторной работы № 3

Принимается также символическая запись синосоидальных колебаний в виде:

U = e ^jwt

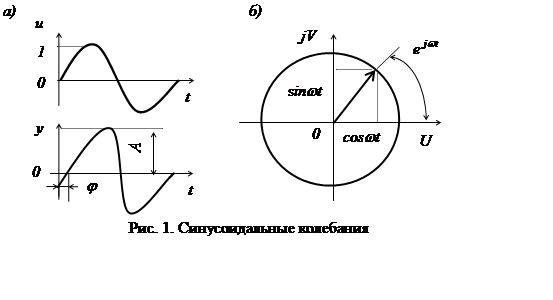
Строго говоря, e ^jwt = cos(wt) + sin(wt), что геометрически изображается вращающимся единичным вектором (рис. 1, б). Проекции последнего на прямоугольные оси дают cos(wt) и sin(wt). Поэтому для суждения о вынужденных синусоидальных колебаниях звена достаточно формально исследовать реакцию звена на символический сигнал e ^jwt.

Для получения частотных характеристик пользуются принципом суперпозиции. Его сущность  заключается в следующем: реакция системы на несколько одновременно действующих входных воздействий равна сумме реакций на каждое воздействие в отдельности. Это позволяет ограничиться изучением систем только с одним воздействием (входом).

В общем случае уравнение линейной стационарной системы с одним входом можно записать так:

(a_орⁿ + а₁р^n-1 + …+ а_n)Y(p) = (b_ор^m + b₁р^m-1 + …+ b_m)U(p).

Ее передаточная функция:

W(p) = Y(p)/U(p) = (b₀p^m + b₁p^m-1 +…+ b_m)/(a₀pⁿ + a₁p^n-1 +…+ a_n).

Функцию W(jw), которую получают из передаточной функции при подстановке в нее p = jw:

W(jw)= (b₀ (jw)^m+b₁(jw)^m-1+…+b_m) /(a₀ (jw)ⁿ+a₁(jw)^n-1+…+a_n),

называют частотной передаточной функцией.

Частотную передаточную функцию (ЧПФ) называют комплекснозначной функцией от действительной переменной w(частоты). ЧПФ можно представить, как комплексную функцию, в алгебраической форме записи:

W(jw) = U(w) + jV(w),

где  U(w) и V(w) – соответственно вещественная и мнимая частотная характеристика системы.

Показательная форма записи:

W(jw) = A(w)e ^jj(w),

где А(w) – модуль; j(w)– аргумент.

Модуль вычисляется по формуле:

А(w) = |W(jw)| = ,

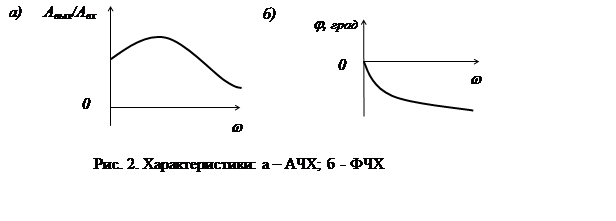
где А(w) – амплитудно-частотная функция, ее график называют амплитудно-частотной характеристикой (рис. 2, а), которая выражает отношение амплитуды колебаний на выходе звена к амплитуде колебаний на его входе в зависимости от частоты выходного сигнала.

Аргумент равен:

j(w) = 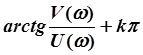;          k = 0; ±1; ±2; ±3;

где j(w)  – фазочастотная функция, ее график называют фазочастотной характеристикой (рис. 2, б). Она выражает зависимость разности фаз между входными и выходными колебаниями звена от частоты входного сигнала. Опережению фазы соответствует j> 0, а отставанию j< 0.

В теории автоматического управления используют комплексную амплитудно-фазовую частотную характеристику (АФЧХ), которая показывает соотношение между амплитудами выходного и входного сигналов и сдвигом фаз  при изменении частоты колебаний входного сигнала от 0 до ¥.

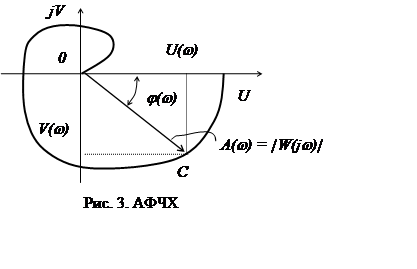
На комплекснозначной плоскости (рис. 3) частотную передаточную функцию определяет вектор ОС, длина (модуль) которого равен амплитуде А(w). Аргумент – угол образованный вектором ОС и положительной действительной осью – j(w).

Кривую, которую описывает конец этого вектора в промежутке [-¥;+¥], называют амплитудно-фазовой частотной характеристикой (АФЧХ).

Частотную передаточную функцию называют также амплитудно-фазовой частотной функцией. Ее действительную часть U(w) = ReW(jw)и мнимую часть V(w) = ImW(jw)называют соответственно вещественной и мнимой частотными функциями.

График зависимости U = U(w) называют действительной частотной характеристикой; график зависимости V = V(w)  называют мнимой частотной характеристикой.

Частотные методы анализа и частотные характеристики применимы только к линейным системам. Однако в ряде случаев их используют и в существенно нелинейных задачах в виде эквивалентных характеристик (метод гармонической линеаризации).

Характеристики можно получить теоретически и экспериментально. Они могут быть использованы для описания свойств отдельных элементов