Построение структурных схем. Определение передаточных функций: Методическое пособие для подготовки и выполнения лабораторной работы № 1

суммирующее) звено окружностью разделенной на четыре сектора. В окружность входят две и выходит одна стрелка, над стрелками ставятся переменные, которые складывают между собой или вычитают друг из друга в зависимости от того, какой стоит знак возле окружности.         

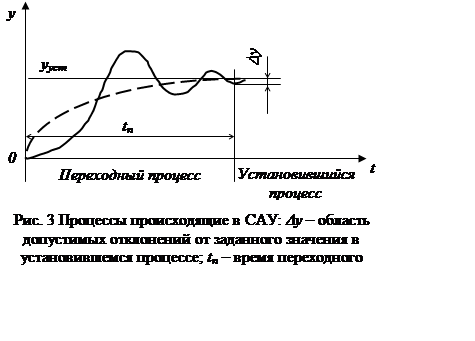
Процессы, происходящие в динамическом звене, делятся на два вида: переходный и установившийся процессы (рис. 3).

Переходный процесс – это процесс, в котором происходит изменение управляемой величины во времени под действием произвольных воздействий, приложенных к системе. Характер переходного процесса зависит от воздействий и свойств системы. Переходный процесс звена или системы характеризуется переходной характеристикой, под которой понимается зависимость выходной величины от времени (t).

К числу воздействий относятся: сигналы скачкообразного (или ступенчатого) характера и сигналы ударного действия, представляющие собой импульсы малой длительности по сравнению с временем переходного процесса.

Чтобы качественно выполнить задачу управления в различных изменяющихся условиях работы, САУ должна обладать заданным определенным запасом устойчивости.

В устойчивых САУ переходный процесс со временем затухает, и наступает установившееся состояние. Установившийся процесс – это равновесный процесс при постоянных воздействиях.

Дифференциальное уравнение звена должно быть составлено так, чтобы оно выражало зависимость между входными и выходными сигналами данного звена в переходном процессе. Физическая задача определения выходной величины звена при изменяющемся входном сигнале сводится к решению дифференциального уравнения того или иного вида, описывающего протекание переходных процессов в звене.

Так как аналитическое решение ДУ в общем случае является трудоемкой задачей, то в современной теории управления широко используют средства описания динамических свойств системы через преобразование Лапласа, что удобнее для практического применения. Основанием для этого служит то обстоятельство, что такое преобразование существенно облегчает исследование сложных систем, заменяя ДУ алгебраическими.

В уравнение (1), содержащее функции времени y(t) и u(t), введем функции Y(p) и U(p) комплексного переменного p=s + jwи поставим условие, что эти функции связаны зависимостями:

Y(p) = 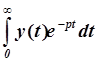,               U(p) = 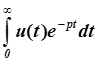.                          (2)

Функция y(t) называется оригиналом функции Y(p), а функция u(t) – оригиналом функции U(p). Операция перехода от исходной функции y(t) к ее изображению Y(p) (нахождение изображения по оригиналу) называют преобразованием Лапласа.

Преобразования оригинала в изображение позволяет свести операции дифференцирования и интегрирования над оригиналами к более простым операциям над их изображениями.

Формально переход от ДУ к алгебраическому операторному уравнению при нулевых начальных условиях (т.е. для t = 0 значение самой функции у(t) и всех ее производных равны нулю) получают путем замены