Математика \ Высшая математика

Приближенное вычисление определенных интегралов. Приближенное вычисление дифференциальных уравнений. Решение нелинейных систем методом итераций. Решение нелинейных систем методом Ньютона

Страницы работы

31 страница (Word-файл)

Посмотреть все страницы

Скачать файл

Фрагмент текста работы

ЛАБОРАТОРНЫЕ РАБОТЫ № 4 - 8

ПО ВЫЧИСЛИТЕЛЬНОМУ ПРАКТИКУМУ

Лабораторная работа № 4

Приближенное вычисление определенных интегралов

Пусть требуется найти определенный интеграл 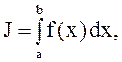где непрерывна на отрезке .

В большинстве случаев решать эту задачу приходится приближенно численными методами, которые основаны на замене подынтегральной функции интерполяционным многочленом. Для достижения необходимой точности вычислений интервал интегрирования делится на более мелкие части и на каждом из этих участков производится соответствующая замена. Тогда весь интеграл 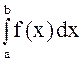представляется в виде линейной комбинации нескольких значений

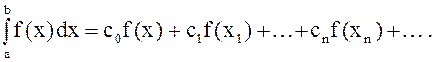
При фиксированном n

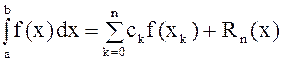
или

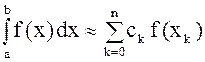(1)

Формулы вида (1) называются квадратурными.

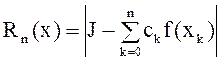называется остаточным членом.

Значения называются узлами или сеткой, n– число разбиений интервала интегрирования.

Если делится на равные части, то 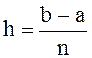называется шагом сетки.

Приближенное значение интеграла будет зависеть от h, поэтому будем обозначать его J(h).

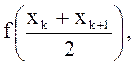
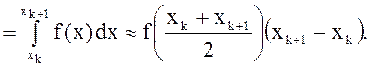Функция на участке заменяется многочленом нулевой степени, т. е. постоянной для всех величиной тогда

Геометрически это означает замену графика

на участке прямой .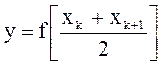

Интеграл, как площадь криволинейной трапеции, будет приближенно равен площади прямоугольника.

Формула прямоугольников:

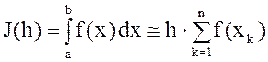. (2)

Остаточный член .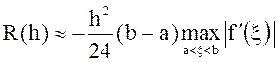

На каждом из участков разбиения заменяется многочленом первой степени. Геометрическая кривая заменяется секущейи интеграл берется приближенно равным площади трапеции с основаниями и высотой

Формула трапеции:

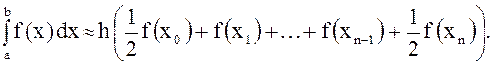(3)

Остаточный член .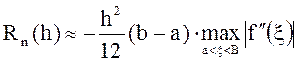

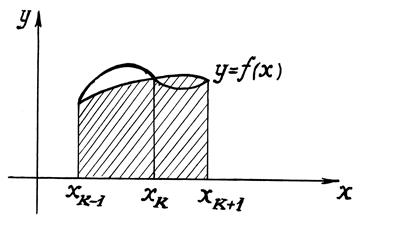
Интервал интегрирования делится на четное число участков, на каждой паре участков с узлами функция заменяется многочленом второй степени, т. е. кривая заменяется квадратичной параболой.

Рис. 1

Формула метода Симпсона:

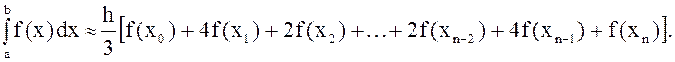(4)

Остаточный член .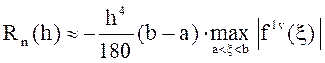

Оценка погрешности и точность вычисления

Погрешность приближенного вычисления интегралов состоит из остаточного члена квадратурной формулы и различных погрешностей округления.

На практике для оценки остаточного члена вычисляют два значения интеграла.

при разбиении интервала интегрирования на n частей и применяют правило Рунге:

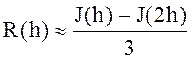для формул прямоугольников и трапеций,

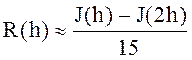для формулы Симпсона. (5)

Здесь - остаточный член (погрешность) более точного значения интеграла .

Чтобы погасить погрешность округления, промежуточные вычисления проводят с одним запасным знаком.

При одном и том же числе разбиений наибольшую точность дает метод Симпсона.

Пусть - заданная точность вычислений, тогда выбирают n таким, чтобы

- для формул прямоугольников и трапеций,

- для формулы Симпсона. (6)

Причём для формул Симпсона должно быть обязательно целым, т. е.

и т. п.

Пример. Вычислить интеграл 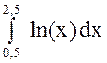с точностью методом Симпсона.

Решение. Вычисление интеграла проводить по следующему плану

1. Выбрать шаг интегрирования. Здесь можно взять n = 16 и h = 0,125.

2. Определить узлы сетки:

3. Для каждого вычислить значение подынтегральной функции

и записать в один из трех столбцов бланка расчета в зависимости от номера k

(табл. 1).

4. Вычислить значение интеграла по формуле (4).

5. Для оценки погрешности вычислить

Заметим, что для этого нужно использовать значение функции только в четных узлах.

6. Определить значение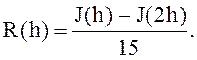

7. Если , то записать в качестве ответа

В противном случае следует повысить точность вычислений одним из двух способов

1. Правило Рунге: если известны два значения интеграла и , то очень хорошую точность можно получить, если к прибавить величину погрешности, найденную по формуле Рунге:

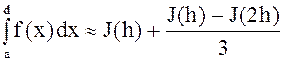- для методов прямоугольников и трапеций,

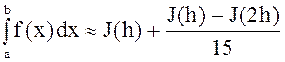- для метода Симпсона. (7)

2. Способ двойного пересчета: увеличим число разбиений n вдвое по сравнению с тем, при котором вычисляли , и найдем новое значение интеграла , если потребуется, то будем уменьшать шаг сетки до тех пор, пока не будут выполняться неравенства

где - заданная точность.

Таблица 1



Номера узлов k	Узлы
Номера узлов k	Узлы	k=0; k=16	k - четные	k - нечетные
0	0,5	0)- 0,69315
1	0,625			- 0,47000
2	0,750		1) – 0,28768
3	0,875			- 0,13353
4	1,000		2) 0,00000
5	1,125			0,11778
6	1,250		3) 0,22315
7	1,375			0,31845
8	1,500		4) 0,40546
9	1,625			0,48551
10	1,750		5) 0,55962
11	1,875			0,62861
12	2,000		6) 0,69315
13	2,125			0,75377
14	2,250		7) 0,81093
15	2,375			0,86500
16	2,500	8) 0,91629
Суммы n=16 n=8		0,22314	2,40463	2,56559
Суммы n=16 n=8		0,22314
Интегралы
Погрешность
Ответ

Задания к лабораторной работе № 4

N	F(x)	a	b
1	2	3	4	5
1		0	1,6	10^-4
2		0	1,6	10^-4
3		0	1,6	10^-4
4		0	1,6	10^-4
5		0	1,6	10^-4
6		0	1,6	10^-4
7		0	3	10^-3
8		0	3	10^-3
9		0	1,6	10^-4
10		0	1,6	10^-4
11		0	3	10^-3
12		1,25	2,45
13		0,5	1,7
14		0,32	1,52
15		1,16	2,72
16		0,3	1,1
17		0,3	1,5
18		0,3	1,5
19		1,7	2,5
20		0,2	1,0
21		1,7	2,9
22		0,7	1,9
23		1,3	2,9
24		0,05	1,65
25		0,1	1,7
26		01	1,7
N	F(x)	a	b
27		2/3	3/5
28		2,3	3,5
29		2,3	3,1
30		1,5	3,1
31		0,3	1,5
32		1,35	2,95
33		0,45	1.25
34		0	1,6
35		0	1,6
36		0,45	1,65
37		0,25	1,45
38		1,2	2
39		0,2	1
40		0,18	0,98
41		0,2	1,8
42		1,4	2,2
43		0,8	1,6
44		0,6	1,4
45		1,2	2
46		2,5	3,3
47		0,5	1,2
48		1,3	2,1
49		0,2	1,0
50		0,8	1,2
51		0,15	0,63
52		1,2	2,8
53		0,6	0,72
54		0,8	1,2