теме: Расчетные схемы балок и определение реакций их опор. 9
Лабораторно – практическое занятие № 3. 14
По теме: Определение главного вектора и главного момента плоской системы произвольно расположенных сил. 14
Лабораторно – практическое занятие № 4. 18
По теме: Определение центра тяжести плоских фигур. 18
Лабораторная работа №5. 25
По теме: Определение траектории, скорости и ускорения. 25
Лабораторно – практическое задание №6. 29
По теме: Расчеты на прочность и жесткость статически определимых брусьев при растяжении – сжатии. 29
Лабораторно – практическое задание № 7. 36
По теме: Испытание на растяжение образца из низкоуглеродистой стали. 36
Лабораторно – практическое задание № 8. 51
По теме: Расчеты на прочность и жесткость при кручении. 51
Лабораторно – практическое задание № 9. 56
По теме: Построение силовых эпюр и расчеты на прочность при изгибе. 56
Цель занятия: научиться находить проекцию силы на ось и равнодействующую системы сходящихся сил аналитическим и геометрическим способом.
Краткая теория.
Система сил, линии, действия которых лежат в одной плоскости и все пересекаются в одной точке, называются плоской системой сходящихся сил.
Плоская система сходящихся сил в общем случае эквивалентна равнодействующей, которая равна векторной сумме этих сил и линия действия равнодействующей проходит через точку пересечения линий действия составляющих.
Существует два способа по определению равнодействующей: геометрический и аналитический.
Геометрический способ заключается в построении силового многоугольника, т. е. в масштабе последовательно откладываются все вектора сил ( из конца первого вектора откладывается второй, из конца второго третий и т. д.). Вектор, соединяющий начало первого с концом последнего вектора будет являться равнодействующей системе сил.
Более точным является аналитический способ, основанный на методе проекции сил.
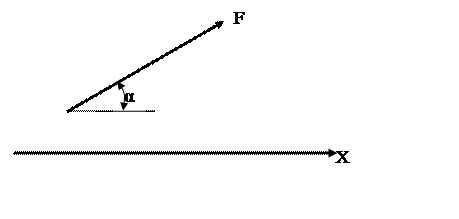
Проекцией силы на ось называется отрезок оси, заключенный между двумя перпендикулярами, опущенными на ось из начала и конца вектора силы.
Проекция силы на ось есть величина алгебраическая, которая может быть положительной или отрицательной, что устанавливается по направлению проекции. За направление проекции принимается направление от проекции начала к проекции конца вектора силы. Если направление проекции силы на ось совпадает с положительным направлением оси, то эта проекция считается положительной.
Если вектор силы параллелен оси, то он проецируется в направленную величину. Если вектор силы перпендикулярен оси, то его проекция равна нулю.
Численно проекция равна произведению модуля силы на косинус угла между направлением силы и положительным направлением оси.
Рис. 1.
Зная проекции силы на две взаимно перпендикулярные оси можно найти модуль силы:
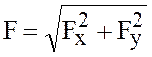
и направление силы
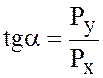, где α – угол с осью х.
Равнодействующая системы сил равна
.
На основании свойства проекции векторной суммы можно утверждать, что проекция равнодействующей на ось равна алгебраической сумме проекций составляющих сил на ту же ось:
, 
,
, 
.
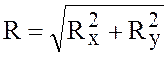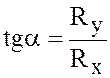Пример.
Дана плоская система сходящихся сил. Найти равнодействующую геометрическим и аналитическим способами.
F1=2Н, F2=4Н, F3=3Н.
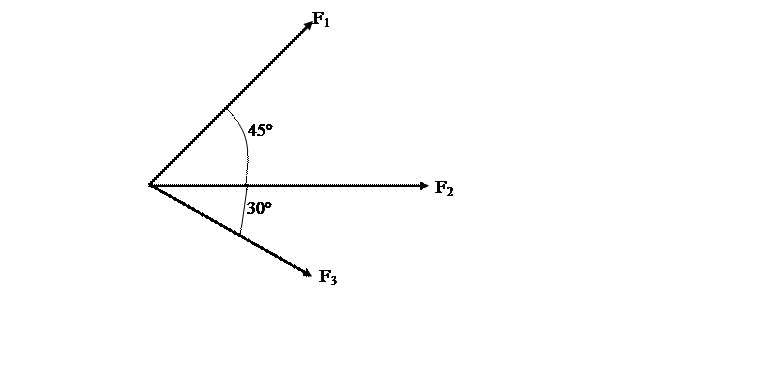
Рис. 2.
Решение.
1. Геометрический способ.
Выбираем для построений масштаб 1Н=1см. С учетом этого масштаба откладываем вектор первой силы под углом 45º к горизонту (2см) затем из конца первого вектора откладываем горизонтально второй вектор (4см), из конца второго вектора откладываем под углом 30º к горизонту третий вектор (3см). Соединяя начало первого вектора и конец третьего, получаем
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
