Пусть дана в отрезке [a,b] непрерывная функция y=f(x), принимающая лишь положительные значения. Рассмотрим фигуру ABCD, ограниченную кривой y=f(x), двумя ординатами x=a и x=b и отрезком оси x; подобную фигуру будем называть криволинейной трапецией. Площадь данной фигуры будет являться определенным интегралом функции f(x) в числовом промежутке [a,b].
f
f(x)
 |
0 a b x
Рассмотрим несколько способов решения данной задачи.
Разделим основание АВ нашей фигуры на произвольное количество равных отрезков и проведем ординаты, соответствующие точкам деления, тогда криволинейная трапеция разобьется на ряд полосок.
Заменим теперь приближенно каждую полоску прямоугольником, основание которого тоже, что и у полоски, а высота совпадает с длиной ординаты проведенной из центра основания полоски. Таким образом криволинейная фигура замениться некоторой ступенчатой фигурой, составленной из отдельных прямоугольников.
f f(x)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
 |
0 a b x
Основание i-го прямоугольника (i = 0, 1, 2, ..., n-1), очевидно, равно разности xi+1 - xi, которую мы будем обозначать через Dxi, что касается высоты, то, по сказанному, она равна yi =f((xi +xi+1)/2). Поэтому площадь i-го прямоугольника будет равна yiDx = f((xi +xi+1)/2)Dxi.
Просуммировав площади всех прямоугольников получим приближенное значение площади S криволинейной трапеции или приближенное значение определенного интеграла.
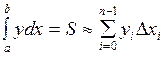 или
или 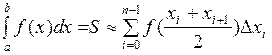 .
.
f f(x)
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
 |
0 a b x
Разделим снова основание АВ нашей фигуры на n теперь уже равных отрезков и проведем ординаты, соответствующие точкам деления и концы их соединим отрезками. В данном случае вычисление интеграла сведется к вычислению площади фигуры, состоящей из множества трапеций.
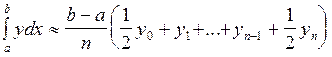
где, yi =f(xi).
или
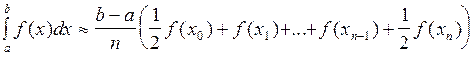 .
.
Формула Симсона
Другой прием вычисления площади S основан на замене частей данной кривой не прямыми, как в правиле трапеций, а дугами парабол, оси которых параллельны оси Y. Получаемая формула называется формулой Симсона..
Площадь первой трапеции равна
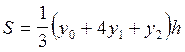 ,
,
где h - расстояние между двумя смежными
ординатами, равное ![]() .
.
Решение нелинейных уравнений вида
F(x)=0
Заключается в отыскании одного или всех корней на отрезке [a,b] изменения x. Обычно стараются локализовать каждый корень в своем отрезке [a,b]. Рассмотрим несколько методов решения данной задачи.
Метод простых итераций основан на представлении функции в виде
x=f(x)
и многократное применение итерационной формулы xn+1=f(x) до тех пор, пока соблюдается условие
|xn+1-xn| ³e,
где e - заданная погрешность вычисления корней .x
Модифицированный метод Ньютона заключается в том, что на каждом шаге итерации находят приближенно значение приближенной значение производной исходной функции. Следовательно, итерационная формула имеет вид
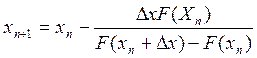 .
.
Значение Dx не обязательно должно быть равно e. Данное равенство позволяет уменьшить число исходных данных при вводе.
Метод хорд. При этом методе каждое значение xn+1 находится как точка пересечения оси абсцисс с хордой, проведенной через точки F(a) и F(b), причем одна из этих точек фиксируется для дальнейшего расчета – та, при использовании которой происходит переход знака в расчетной функции F от конечных точек. Если это точка a, то
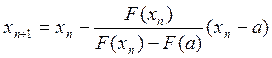 ,
,
в противном случае
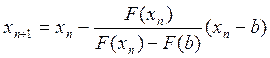 .
.
Если
|xn+1-xn| ³e,
то в первом случае считаем b = xn+1, во втором a = xn+1 и повторяем вычисления.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.