Решение слабо- и неструктуризованных задач

Если условие выполняется, значит, вычисления были правильными.

 – выполняется.

Критерий 3:

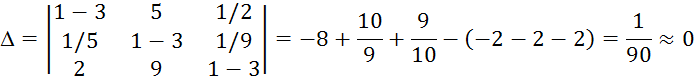
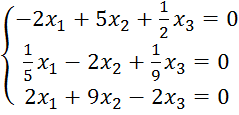
Пусть , тогда

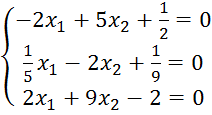
Сложим первое и третье уравнения. В результате получаем уравнение с одной неизвестной – х₂, которую легко найти, решив данное уравнение:

Зная х₂ и х₃, можно найти х₁, выразив его из любого уравнения (в данном случае – из второго):

В результате вычислений получаем собственный вектор .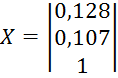

В сумме веса дуг должны составлять единицу. Если условие выполняется, значит, вычисления были правильными.

 – выполняется.

Критерий 4:

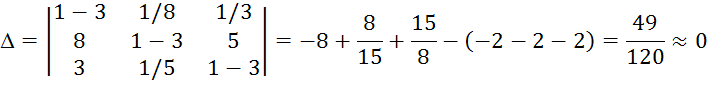
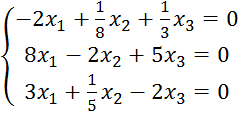
Пусть , тогда

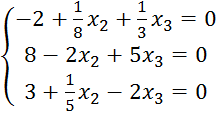
Умножим третье уравнение на 10, получим:

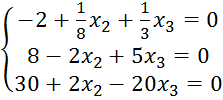
Сложим второе и третье уравнения. В результате получаем уравнение с одной неизвестной – х₃, которую легко найти, решив данное уравнение:

Зная х₁ и х₃, можно найти х₂, выразив его из любого уравнения (в данном случае – из второго):

В результате вычислений получаем собственный вектор .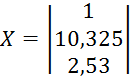

В сумме веса дуг должны составлять единицу. Если условие выполняется, значит, вычисления были правильными.

 – выполняется.

Критерий 5:

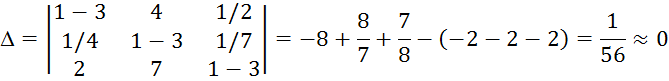
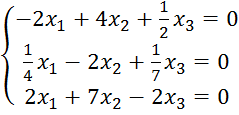
Пусть , тогда

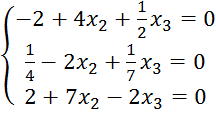
Умножим первое уравнение на 4, получим:

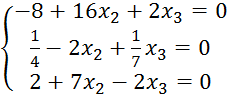
Сложим первое и третье уравнения. В результате получаем уравнение с одной неизвестной – х₂, которую легко найти, решив данное уравнение:

Зная х₁ и х₂, можно найти х₃, выразив его из любого уравнения (в данном случае – из третьего):

В результате вычислений получаем собственный вектор .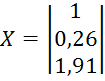

В сумме веса дуг должны составлять единицу. Если условие выполняется, значит, вычисления были правильными.

 – выполняется.

2.4.  Рассчитать веса элементов иерархии  и принять решение на основе полученных результатов.

 (1 уровень иерархии)

 (2 уровень иерархии)

 (3 уровень иерархии)

Сумма значений каждого уровня должна быть равна 1.

 – выполняется.

 – выполняется.

ВЫВОД: наилучшей альтернативой по МАИ для решения данной проблемы является третья ().

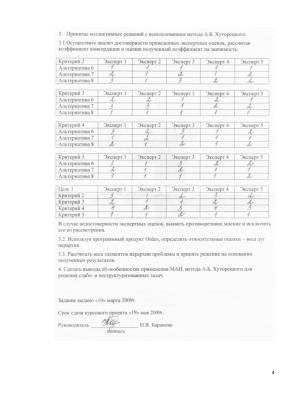
3.  Принятие коллективных решений с использованием А.Б. Хуторецкого.

При оценке плохоквантифицируемых свойств объектов эксперты вынуждены в значительной степени использовать интуицию. В данном случае средств верификации данных нет, поэтому главное требование к экспертным процедурам состоит в максимальной простоте задаваемых вопросов.  В наибольшей степени этому требованию удовлетворяет процедура попарного сравнения объектов. Для оценки n объектов необходимо произвести  сравнений. При больших n – высокая трудоемкость расчетов. Чем больше матрица, тем более сложным является обеспечение транзитивности. Избавиться от излишней трудоемкости за счет минимального усложнения задаваемых вопросов, позволяет процедура ранжирования.

Суть процедуры: каждому эксперту предъявляются сразу все объекты, которые он должен упорядочить по снижению их качества (важности, предпочтительности, значимости) в отношении рассматриваемого критерия. При этом некоторые объекты эксперт может признать неразличимыми, т.е. эквивалентными.

3.1.  Осуществить анализ достоверности приведенных экспертных оценок, рассчитав коэффициент конкордации и оценив полученный коэффициент на значимость. В случае недостоверности экспертных оценок, выявить и исключить противоречивое мнение.

Статистическая обработка информации, полученной от экспертов, включает в себя анализ ее на достоверность.

Достоверность оценок гарантируется, если действия экспертов достаточно согласованы. Методологические различия процедуры оценки согласованности определяются характером получаемой в процессе экспертизы информации.

Для оценки согласованности мнений экспертов относительно ранжированных объектов, используются коэффициент конкордации, расчет которого при совпадении ранговых оценок у одного и того же эксперта, производится по формуле:

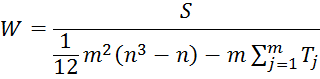
где S – сумма квадратов отклонений, определяется по формуле:

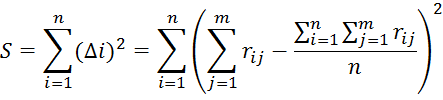
r_ij – оценка экспертом j объекта i

n – количество ранжируемых объектов

m – число экспертов

T_j – параметр, определяемый по формуле:

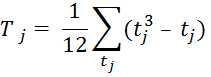
t_j – количество одинаковых рангов в j-м ряду

Обязательным условием использования методов ранговой корреляции в отношении ранжированных объектов является равенство числа рангов числу оцениваемых объектов, т.е. сумма рангов должна быть равна:

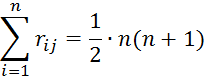
Выполнение данного условия позволяет обеспечить стандартное ранжирование. Объектам, имеющим одинаковый ранг, присваиваются стандартизированные ранги, значение которых, представляет собой среднее место, поделенных между собой объектами с одинаковыми рангами.

Если коэффициент конкордации достиг необходимого  значения (0,7 и более), то необходимо проверить его на значимость.

Проверка коэффициента конкордации на значимость

Считается, что величина mW(n – 1) имеет -распределений