Решение задач транспортного типа методами северо-западного угла, минимального элемента, двойного предпочтения, потенциалов и венгерским методом, страница 5

В нижней строке полученной таблицы есть положительный элемент, поэтому продолжаем искать оптимальное решение.  Выбираем разрешающий элемент. Пусть разрешающим будет элемент, расположенный в клетке (x₂; y₁) и равный 63/12. Обведем его. Вычислим его обратную величину λ = и поставим ее в нижнюю часть клетки. Все элементы разрешающей строки (строка, в которой стоит разрешающий элемент) кроме самого разрешающего элемента умножаем на , а все элементы разрешающего столбца умножаем на  и записываем значения в нижние части клеток. В разрешающей строке выделяем все прежние элементы (стоящие в верхней части клеток) кроме разрешающего, а в разрешающем столбце – все новые (стоящие в нижней части клеток). В нижнюю часть клетки, не принадлежащей ни разрешающей строке, ни разрешающему столбцу, записываем произведение выделенных элементов и расположенной в строке и столбце, что и эти элементы.

Чертим новую таблицу с новым набором свободных переменных. Меняем местами x₂ и y₁. Элементы разрешающих строки и столбца заменяем элементами, стоящими в нижних частях тех же клеток предыдущей таблицы. В остальных клетках новой таблицы записываем алгебраическую сумму элементов, стоящих в верхних и нижних частях соответствующих клеток прежней таблицы.

Все элементы нижней строки новой таблицы отрицательны, значит оптимальное решение найдено.

, что приблизительно равно x₁=5.2 из графического решения.

, что приблизительно равно x₂=5 из графического решения.

, что приблизительно равно W=91.8 из графического решения.

Двойственный метод:

108y₁ + 108y₂ → min   (5)

9y₁ + 12y₂  ≥ 9               (6)

12y₁ + 9y₂  ≥ 9               (7)

y₁ ≥ 0, y₂ ≥ 0                  (8)

Решим задачу графическим способом.

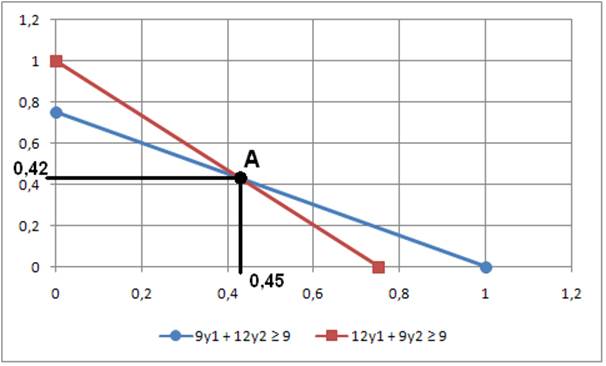
По построенному графику можно определить координаты точки пересечения

A ≈ (0,45; 0,42). Отсюда можно вычислить значение W=108*0,45+108*0,42=93,96.

Решим задачу симплекс-методом. Для этого строим симплекс-таблицу и заполняем ее аналогично прямому методу.

Все элементы нижней строки новой таблицы отрицательны, значит оптимальное решение найдено.

, что приблизительно равно y₁=0.45 из графического решения.

, что приблизительно равно y₂=0.42 из графического решения.

, что приблизительно равно W=93.96 из графического решения.

Вывод: Так как обе эти задачи связаны между собой, то решение прямой задачи одновременно приводит к решению двойственной к ней. Обе задачи представляются одной и той же симплекс-таблицей, хотя условия выбора ведущего элемента для каждой из задач различны. Отсюда следует, что двойственная задача противоположна прямой.