Решение задач транспортного типа методами северо-западного угла, минимального элемента, двойного предпочтения, потенциалов и венгерским методом, страница 4

Считаем Z.

Z =6*2+10*15+6*5+9*5+11*6+3*26+13*4+2*8=449

Вывод: Решая транспортную задачу методом северо-западного угла, получили максимальное значение целевой функции (Z=527). Оптимальный план перевозок был получен методом минимального элемента, двойственного предпочтения и венгерским (Z=449). Метод потенциалов дал значение целевой функции (Z=473).

Методы решения задач линейного и целочисленного программирования

Задание:

8x₁ + 8x₂ → max  (1)

8x₁ + 11x₂ ≤ 88   (2)

11x₁ + 8x₂ ≤ 88   (3)

x₁ ≥ 0, x₂ ≥ 0         (4)

Прямой метод:

Решим задачу графическим способом.

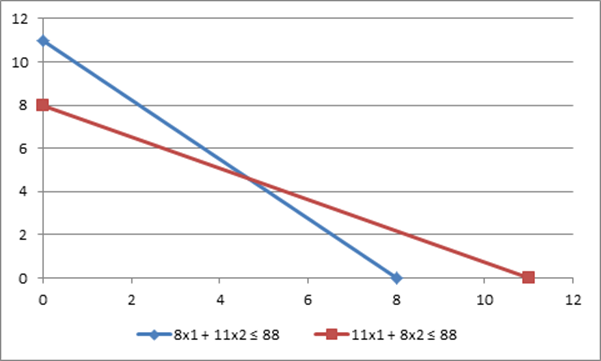
По построенному графику можно определить координаты точки пересечения A ≈ (5,2; 5). Отсюда можно вычислить значение W=9*5,2+9*5=91,8.

Решим задачу симплекс-методом. Для этого строим симплекс-таблицу.

В первом столбце – базисные переменные Y₁, Y₂ и L. Во втором столбце – свободные члены из уравнений (1), (2) и (3). В остальных клетках записываем соответствующие коэффициенты перед свободными переменными. Коэффициенты и свободные члены записываем в верхней части клеток таблицы.

Выбираем разрешающий элемент, который должен быть положительным и давать наименьшее возможное значение при делении на него соответствующего свободного члена: 108/9=12; 108/12=9. Пусть разрешающим будет элемент, расположенный в клетке (x₁; y₂) и равный 12. Обведем его. Вычислим его обратную величину λ = и поставим ее в нижнюю часть клетки. Все элементы разрешающей строки (строка, в которой стоит разрешающий элемент) кроме самого разрешающего элемента умножаем на λ, а все элементы разрешающего столбца умножаем на –λ и записываем значения в нижние части клеток. В разрешающей строке выделяем все прежние элементы (стоящие в верхней части клеток) кроме разрешающего, а в разрешающем столбце – все новые (стоящие в нижней части клеток). В нижнюю часть клетки, не принадлежащей ни разрешающей строке, ни разрешающему столбцу, записываем произведение выделенных элементов и расположенной в строке и столбце, что и эти элементы.

Чертим новую таблицу с новым набором свободных переменных. Меняем местами x₁ и y₂. Элементы разрешающих строки и столбца заменяем элементами, стоящими в нижних частях тех же клеток предыдущей таблицы. В остальных клетках новой таблицы записываем алгебраическую сумму элементов, стоящих в верхних и нижних частях соответствующих клеток прежней таблицы.

Теперь проделываем все операции до тех пор пока не будет получено оптимальное решение, когда все элементы нижней строки таблицы станут отрицательными или равными нулю.