Сравнение эффективности двух технологических процессов

Федеральное агентство по образованию Российской Федерации

ГОУ ВПО «Сибирский государственный технологический университет»

Химико-технологический факультет

Кафедра системотехники

Лабораторная работа № 1

Сравнение эффективности двух технологических

процессов

Руководитель:

________________Г.И. Сорокина

(подпись)

_______________________

(оценка, дата)

Разработал:

Студент группы 64-4

Осадчая О.В.

Михальцевич А.Н..

 (подпись)   

__________________________ (дата)

Условие задачи.

        На лабораторной установке в оптимальном режиме было получено химическое вещество по двум различным способам. По каждому способу проводилась серия параллельных опытов. Выход химического продукта в % полученного по первому и второму способам приведен в таблице 1. Определить, какой способ получения данного химического вещества более эффективен.

Таблица 1

Описание алгоритма расчета и его результаты

Расчет проводится в следующей последовательности:

1.       Проверка анормальности результатов.

а) вычисляем по формулам математическое ожидание, выборочную дисперсию и среднеквадратическое отклонение выборок Х₁ и Х₂;

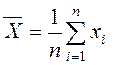
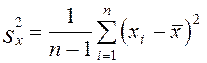
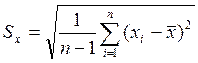
Математическое ожидание:

;                         ;

Выборочная дисперсия:

;                                

Среднеквадратическое отклонение:

;                           ;

б) Вычисляем статистики по формулам для выборок X₁  и X₂:

                            

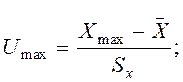
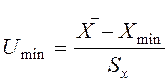
для выборки  получаем:

для выборки  получаем:

По таблице находим квантиль распределения b при объеме выборки равном 8 и 11 уровне значимости a = 0,05

b₁=2.11                b₂=2.29

Так как U_max≤β, то делаем вывод, что результаты однородны, попадают в доверительный интервал, а если и выходят, то не более, чем на 5%

2.       Проверка однородности двух дисперсий

Производится по критерию Фишера, кот. зависит от степени свободы числителя и знаменателя:

а) вычисляем расчетный критерий Фишера по формуле

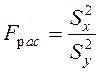
F_табл.= 3,35;  

при числе степеней свободы числителя (выборка X₂) f₂=n – 1=12––1=11, a знаменателя (выборка X₁) f₁=(n – 1) = 9 – 1 =8, уровень значимости  a =0.05

F_расч.<F_табл.;                     1,212254549 < 3,35

Следовательно, дисперсии однородны, ошибка менее 5% и можно продолжать расчеты дальше.

3.       Сравнение двух средних арифметических

а) Поскольку дисперсии однородны, можно вычислить среднюю дисперсию двух выборок по формуле

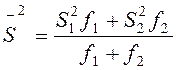
б) рассчитываем критерий Стьюдента по формуле

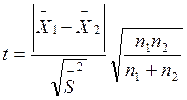
t_табл. = 2.09 при числе степеней свободы f = f₁+ f₂=8 + 11 = 19 и уровне значимости           a=0.05

t_расч.= 0,301120499 < t_табл.= 2,09 ,

Следовательно, X₁ и X₂ являются оценкой одного генерального

математического ожидания и выборки X₁ и X₂, относятся к одной генеральной совокупности.

Вывод: с вероятностью допустить ошибку, равной 5%, можно утверждать, что получение химического вещества двумя различными способами дает одинаковое количество продукта, то есть имеет одинаковую эффективность. 

№ опыта	Выход хим в-ва
	1 способ	2 способ
	X1	X2
1	62,7	64,3
2	65,3	61,1
3	61,4	60,4
4	64,4	62,3
5	64,7	62,4
6	62	62,3
7	62,9	61,3
8	65,1	60,2
9	65,6	64,8
10		61,1
11		62,8
12		62,3
математическое ожидание	63,78889	62,10833
Дисперсия	2,421111	1,997197
ср. квадратическое отклонение	1,555992	1,413222
Umax	1,163959	1,904631
Umin	1,535284	1,350342
β	2,11	2,29
обе выборки однородны
Fрасч	1,212254549
Fтабл	3,35
степень свободы	8	11
обе дисперсии однородны
Средняя дисперсия двух выборок	160,1878472
Критерий Стьюдента tрасч	0,301120499
tтабл	2,09
х1 и х2 являются оценкой одного  генерального математического ожидания и выборки х1 и х2 относятся к одной генеральной совокупности
Вывод:  эффективность процессов одинакова.