Разработка математической модели и оптимального режима технологического процесса получения максимального выхода химического вещества

коэффициенты в уравнении регрессии в каноническом виде;

 X_i – канонические переменные, являющиеся линейными функциями факторов х_i.

Схема перевода в канонический вид:

а) определяем координаты центра поверхности отклика

Для этого необходимо решить систему нормальных уравнений (количество уравнений равно количеству факторов):

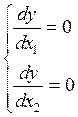                                                                                              (1.19)

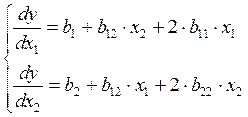                                                         (1.20)

Решая систему, находим координаты центра поверхности х_1s и х_2s. Центр обозначим через s.

                                                                            (1.21)

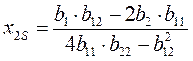                                                                            (1.22)

где х_1s, х_2s – координаты центра поверхности.

Затем в уравнение регрессии в кодированном виде (1.17) подставляем х_1s, х_2s вместо х₁, х₂ получаем У_s, координату центра поверхности отклика. Центр поверхности и центр плана никогда не совпадают.

б) переводим начало координат в центр поверхности отклика, при этом старые координаты будут связаны с новыми соотношением:

x₁=x_1s+х'₁              х₂=х_2s+х'₂,             у=у_s+у'                           (1.23)

Эти формулы подставляем в уравнение регрессии, проводим преобразования и получаем уравнение

y–y_s=b₁₂ х₁' х₂'+b₁₁(х₁')²+ b₂₂(х₂')²                                            (1.24)

в) линейные факторы убрали и остались факторы взаимодействия для этого необходимо систему координат повернуть на угол a до совмещения с осями эллипса.

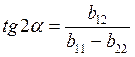                                                                            (1.25)

Переводим старые координаты в новые по формулам:

х₁ =(Х₁ + х_1s)соsα–(Х₂ +х_2s)sinα;

х₂ =(Х₁ +х_1s)sinα + (Х₂ +х_2s)соsα.                             (1.26)

где Х_i – значение фактора в каноническом виде.

Подставляем x₁ и х₂ в уравнение (1.24) и получаем уравнение в каноническом виде.

г) вычисляем канонические коэффициенты В_i

Для расчёта составляем характеристический детерминант (определитель)

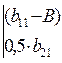
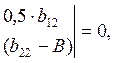                                                           (1.27)

Определитель приравниваем к нулю и решаем, получаем уравнение

                                                              (1.28)

Вычисляем корни полученного квадратного уравнения

Ax²+Bx+C=0                                                                   (1.29)

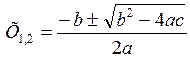                                                         (1.30)

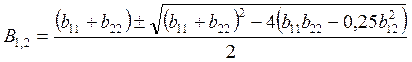                                        (1.31)

где B_1,2 – коэффициенты канонического уравнения.

Если коэффициенты имеют одинаковые знаки, то поверхность – эллиптический параболоид. Если B_ii>0 – ветви направлены вверх, если B_ii<0 – вниз.

Если коэффициенты имеют разные знаки, то поверхность гиперболический параболоид.

Если один из коэффициентов B_ii близок или равен нулю, при этом центр поверхности далеко за границами исследования, поверхность при этом возвышающийся “гребень”. Центр поверхности уходит в бесконечность.

В зависимости от поверхности используем тот или иной метод оптимизации.

При исследовании поверхности и оптимизации процесса выбирают два фактора наиболее влияющих на процесс, и по ним проводят исследование и оптимизацию, остальные значимые факторы стабилизируют на центральном уровне.

Если поверхность эллиптический параболоид, то выбор оптимального режима не представляет трудностей. В случае задачи на B_ii<0, y_max вычисляем координату центра поверхности – это и есть оптимальный режим. B_ii>0, y_min оптимальный режим лежит на эллипсе и ограничивается областью факторного пространства +a и –a.

Если поверхность гиперболический параболоид, применяют два метода оптимизации:

1. Метод ”Ридж-анализ”, базируется на методе неопределённых множителей Лагранжа

Для расчёта оптимального режима необходимо составить систему уравнений, где количество уравнений равно количеству факторов

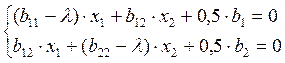                                                               (1.32)

где λ – неопределённый множитель Лагранжа.

Формулы для вычисления x₁ и x₂:

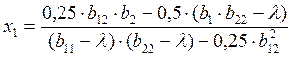
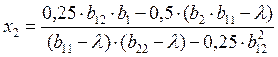                                                               (1.33)

λ задаётся исследователем. В случае задачи на y_max рекомендуется выбирать значение λ таким, чтобы оно было больше коэффициента B_ii (канонического) и наоборот, в случае задачи на y_min – меньше наименьшего канонического коэффициента B_ii.

λ >B_max                                                                               (1.34)

  λ <B_min

На изменение неопределённого множителя Лагранжа накладывается ограничение, определяемое параметром Хорля

λ'=2(В_mах–b_kk),               λ'=2(В_min–b_kk),                                    (1.36)

где λ' – параметр Хорля;

 b_kk – коэффициент, оставшийся в кодированном виде.

λ'λ>B_max                                                               (1.37)

 λ'λ<B_min

Далее подставляем x₁ и x₂ в уравнение (1.17), вычисляем значение y. Если полученный расчетный y совпадает с желаемым, то х₁ и х₂ соответствуют оптимальному режиму. Если не получили желаемый результат, то изменяем значение множителя Лагранжа, пока желаемый результат не будет достигнут.

Переводим оптимальный режим в кодированном виде в натуральный вид по формуле:

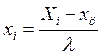                                                                                        (1.38)

где l – интервал варьирования;

 х_ц – центральный уровень фактора;

X_i – значение фактора в натуральном виде;

x_i – значение фактора в кодированном виде.

2. Метод движения вдоль канонических осей

Исходные данные для метода является уравнение регрессии в каноническом виде. В соответствии с поставленной задачей в канонической системе координат, выбираем ось, вдоль которой параметр оптимизации