



Методическое указание по курсу ОТД
Целью практического занятия является изучение принципов организации функционального контроля комбинационного дискретного устройства (КДУ) с помощью методов дублирования и паритета. Перед выполнением практического занятия студентам необходимо ознакомиться с содержанием разделов 6.1, 6.2 и 6.3 учебника [1]. Получить у преподавателя вариант задания (номер комбинационной схемы и номера элементов). Неисправности типа “константа 0” и “константа 1” на выходах заданных элементов рассматриваются при выполнении задания. Далее приводится последовательность выполнения задания.
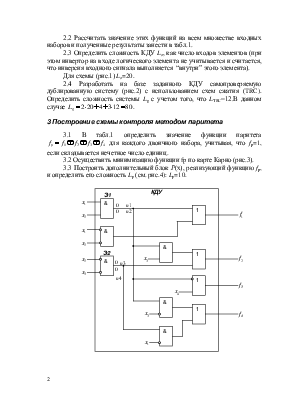
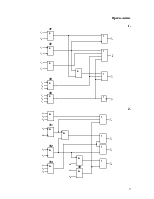
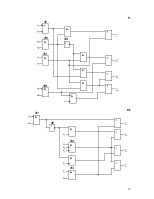
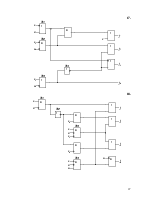
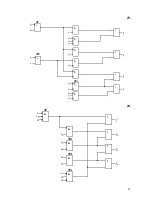
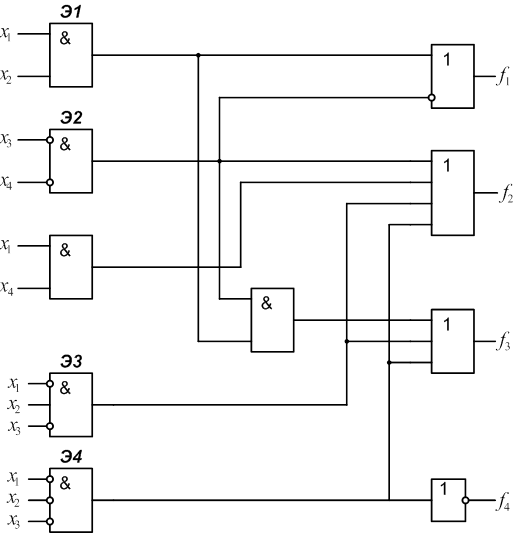
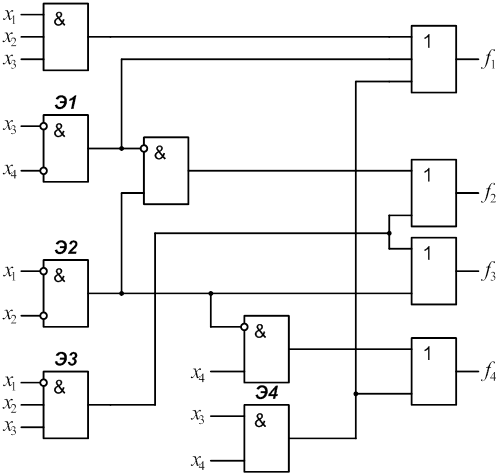
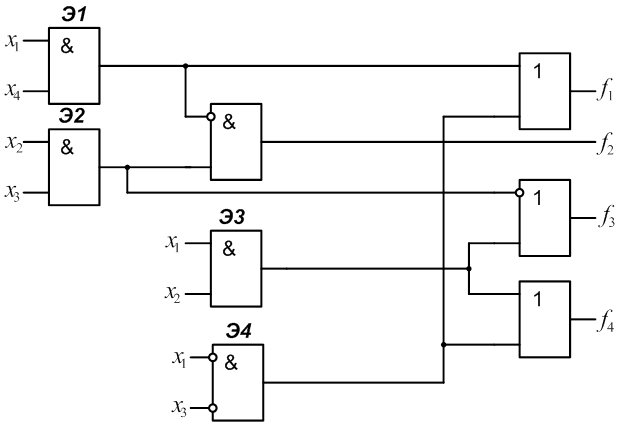
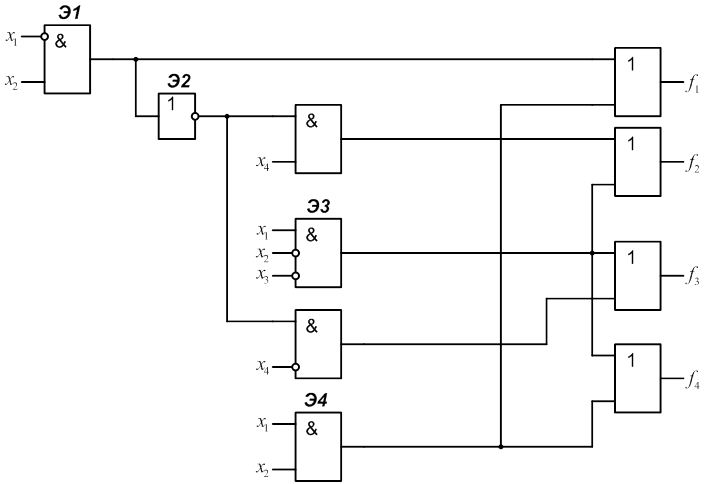
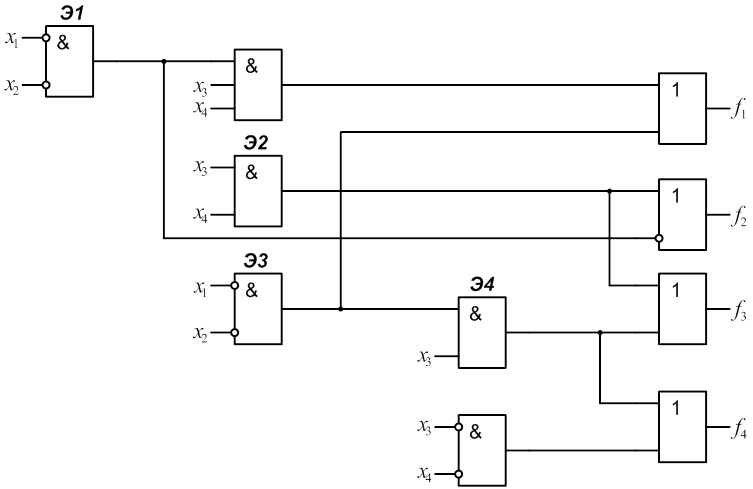
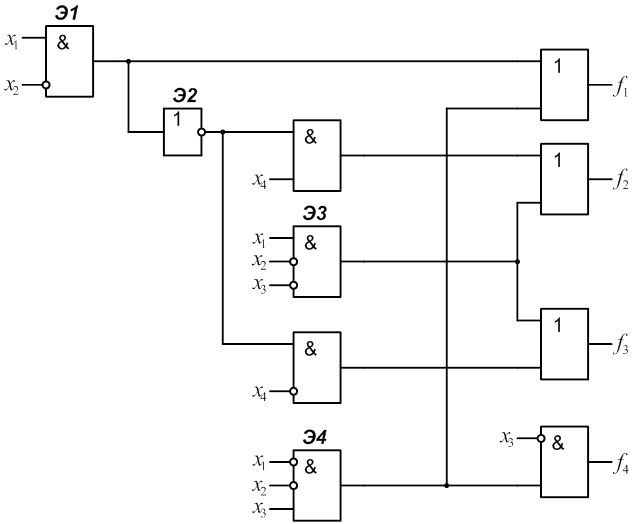
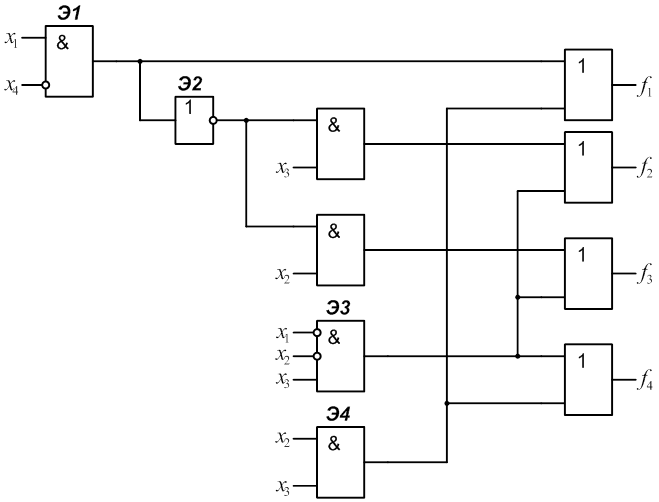
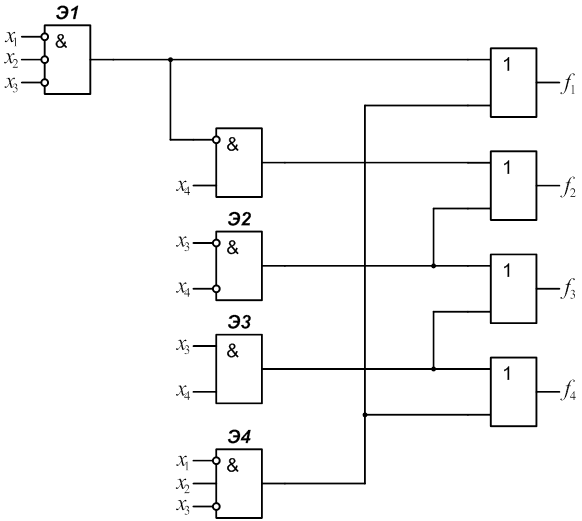
2.1 Для заданного КДУ (рис.1) определить реализуемые на его выходах функции алгебры логики f1, f2, f3, f4.
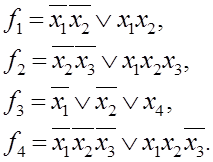
2.2 Рассчитать значение этих функций на всем множестве входных наборов и полученные результаты занести в табл.1.
2.3 Определить сложность КДУ Lо, как число входов элементов (при этом инвертор на входе логического элемента не учитывается и считается, что инверсия входного сигнала выполняется “внутри” этого элемента).
Для схемы (рис.1) Lо=20.
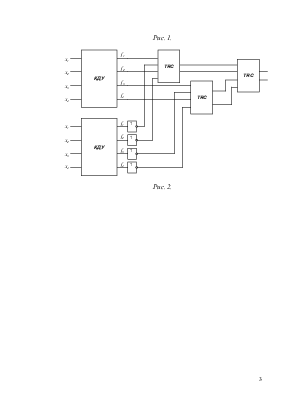
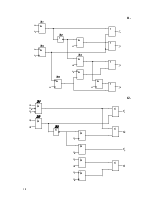
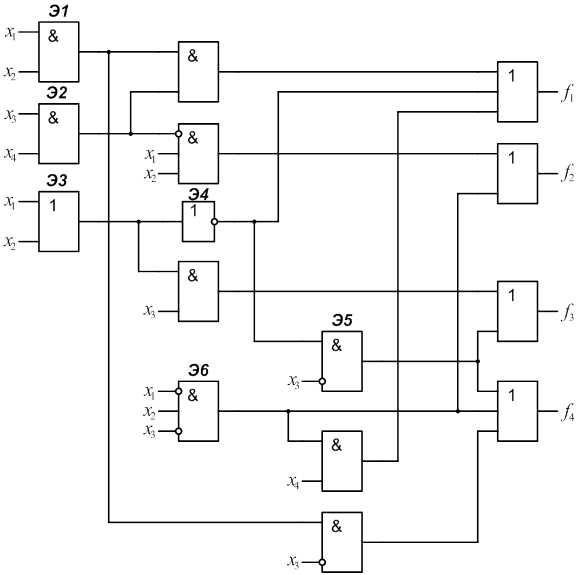
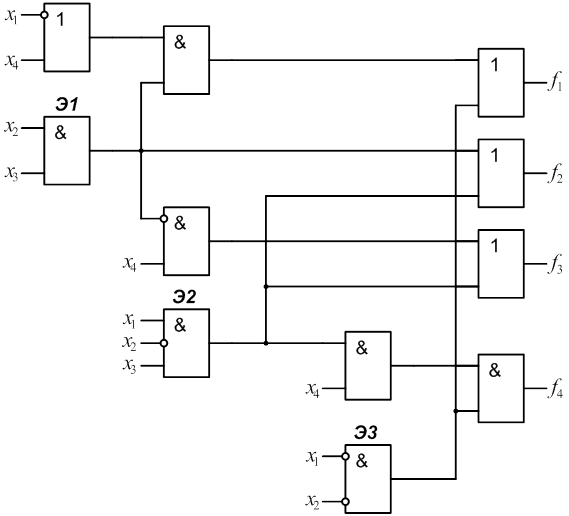
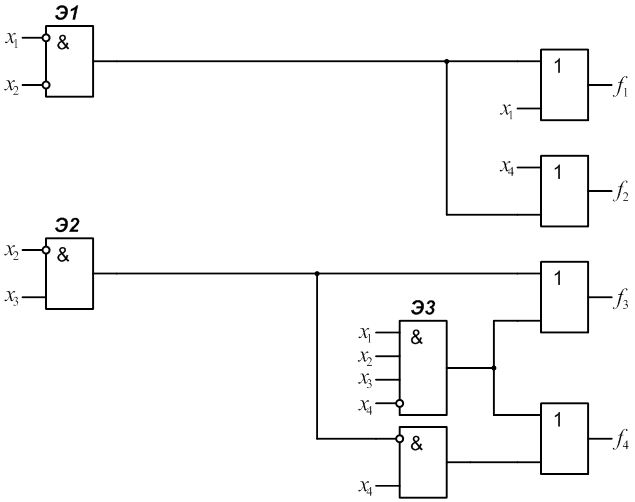
2.4 Разработать на базе заданного КДУ самопроверяемую
дублированную систему (рис.2) с использованием схем сжатия (TRC).
Определить сложность системы Lg
с учетом того, что LTRC=12.В данном случае ![]() .
.
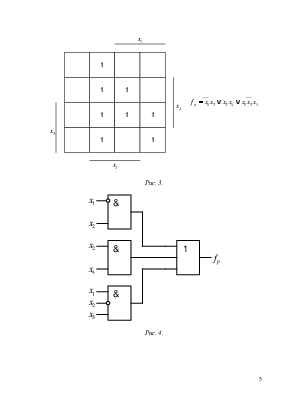
3.1 В табл.1 определить значение функции паритета ![]() для каждого двоичного набора, учитывая, что fp=1, если
складывается нечетное число единиц.
для каждого двоичного набора, учитывая, что fp=1, если
складывается нечетное число единиц.
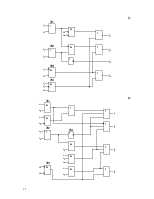
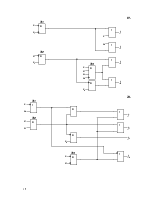
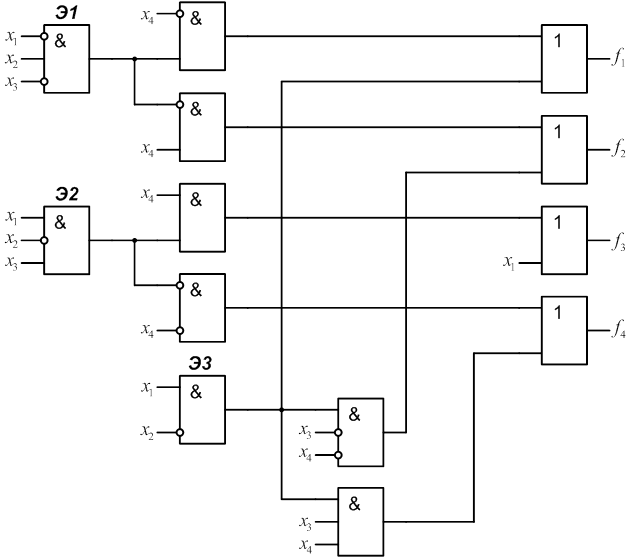
3.2 Осуществить минимизацию функции fp по карте Карно (рис.3).
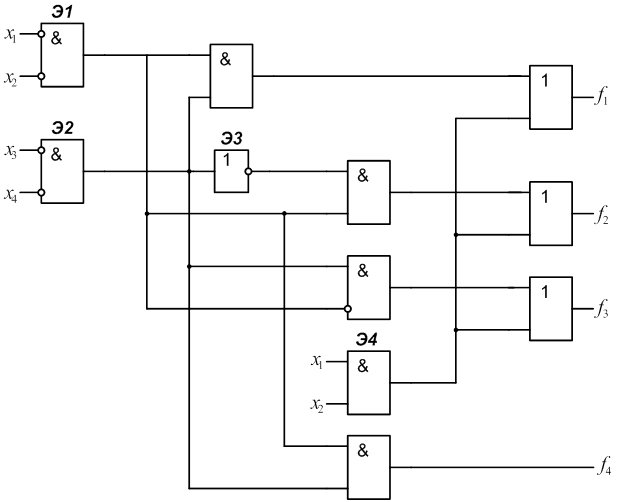
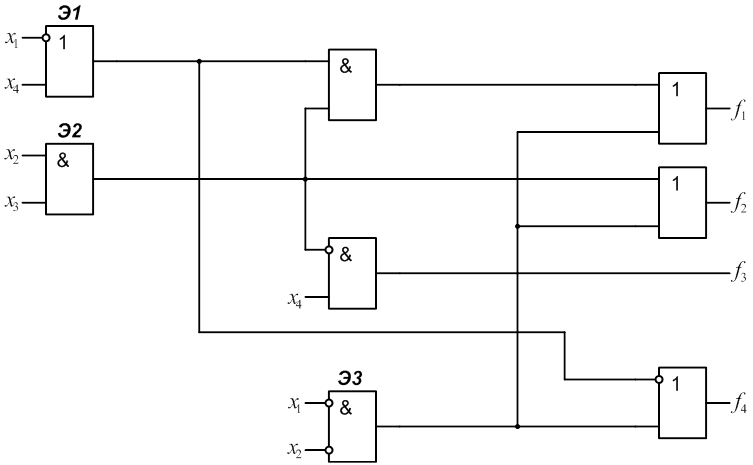
3.3 Построить дополнительный блок Р(х), реализующий функцию fp, и определить его сложность Lр (см. рис.4): Lр=10.
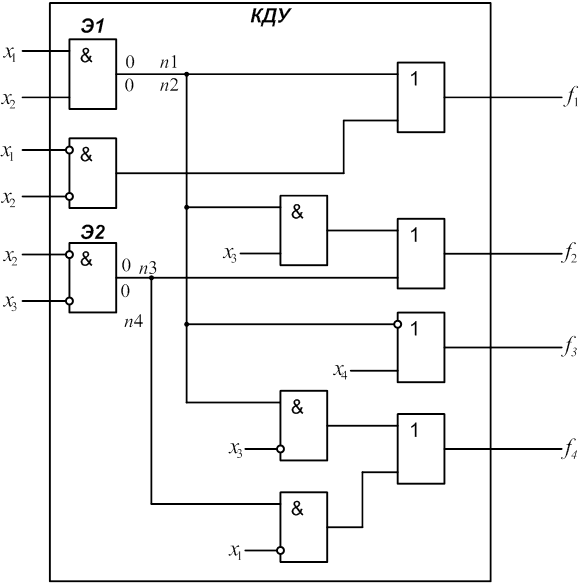
Рис. 1.
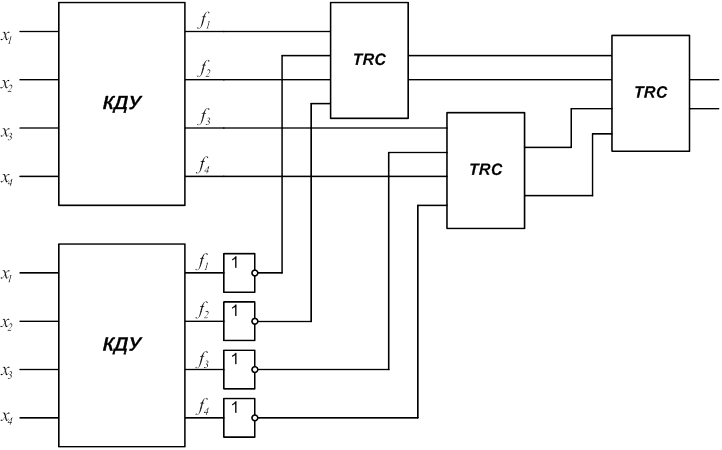
Рис. 2.

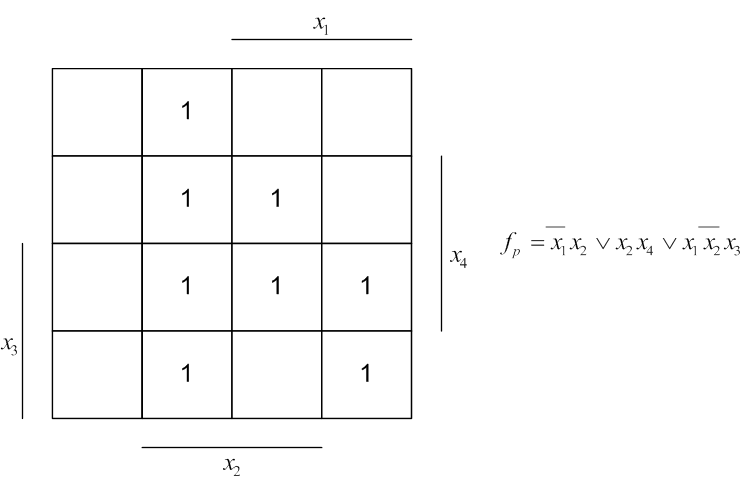
Рис. 3.
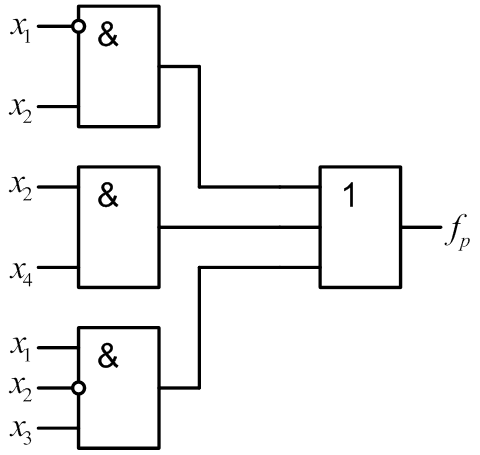
Рис. 4.
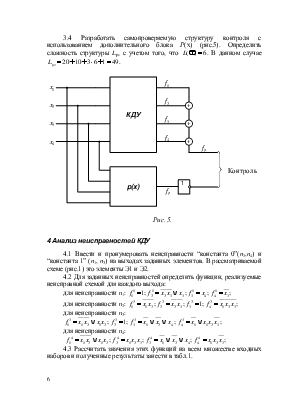
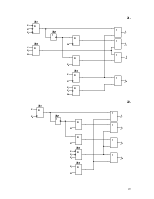
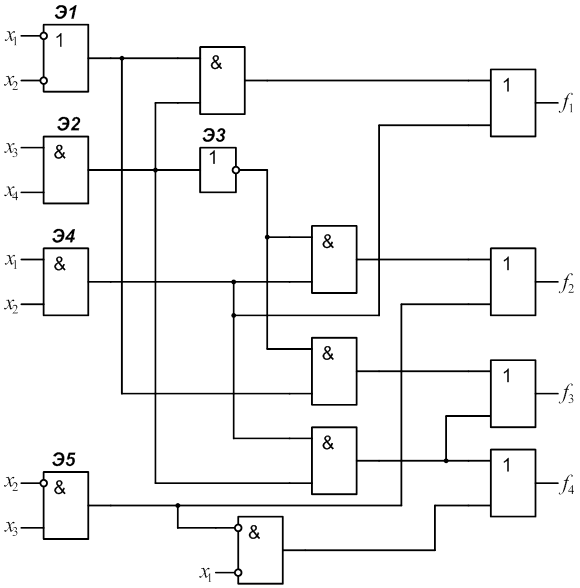
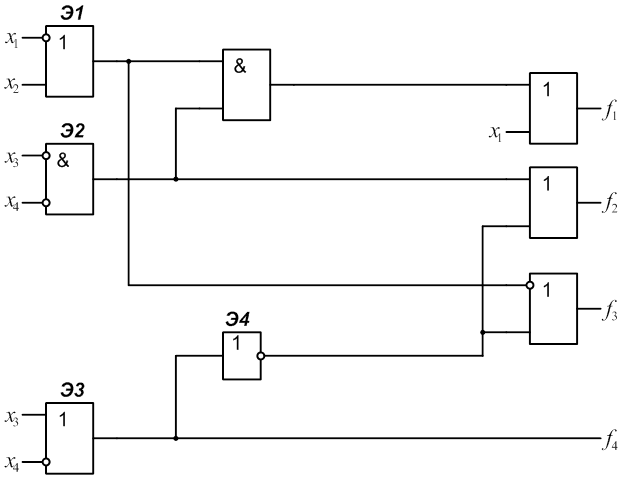
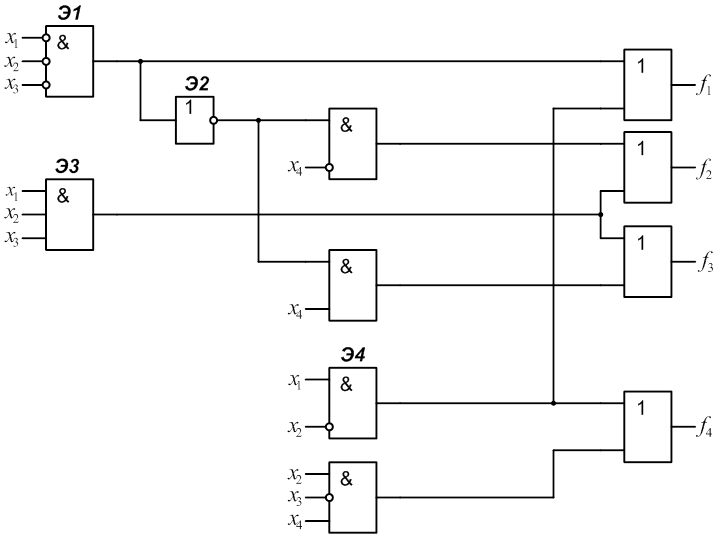
3.4 Разработать самопроверяемую структуру контроля с
использованием дополнительного блока Р(х) (рис.5). Определить сложность
структуры Lрс с
учетом того, что ![]() . В данном случае
. В данном случае ![]() .
.
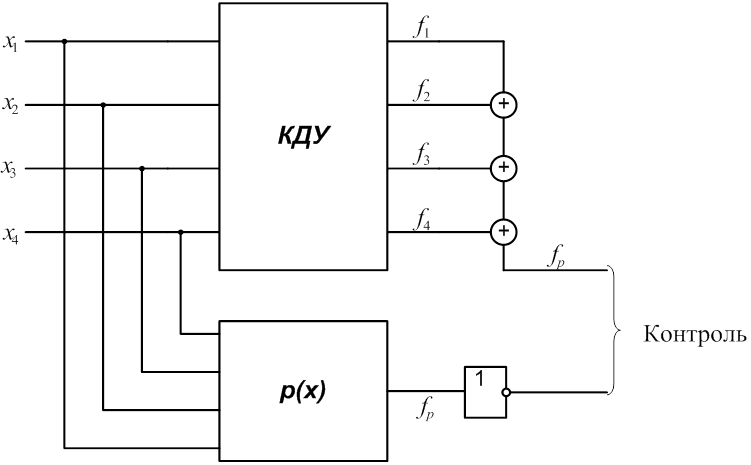
Рис. 5.
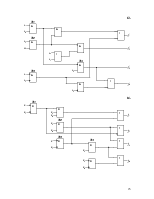
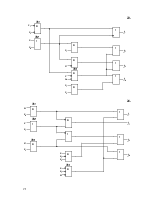
4.1 Ввести и пронумеровать неисправности “константа 0”(n2,n4) и “константа 1” (n1, n3) на выходах заданных элементов. В рассматриваемой схеме (рис.1) это элементы Э1 и Э2.
4.2 Для заданных неисправностей определить функции, реализуемые неисправной схемой для каждого выхода:
для неисправности n1: ![]()
для неисправности n2: ![]()
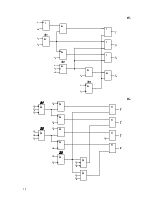
для неисправности n3:
![]()
для неисправности n4:
![]()
4.3 Рассчитать значения этих функций на всем множестве входных наборов и полученные результаты занести в табл.1.
4.4 Путем анализа табл.1 определить для каждой из неисправностей обеих систем функционального контроля те входные наборы, на которых происходит искажение выходных функций f1, f2, f3, f4 в КДУ, но которые не обнаруживаются соответствующей схемой контроля. Полученные результаты занести в табл.2.
Таблица 2
|
Неисправность |
Номера входных наборов, на которых неисправность не обнаруживается |
|
|
Дублирование |
Паритет |
|
|
n1 |
Обнаруживаются все одиночные неисправности на всех входных наборах |
2,5,7,9,11 |
|
n2 |
13,15 |
|
|
n3 |
2,3,4,5,6,7 |
|
|
n4 |
0,1 |
|
4.5 Произвести в табл.3 сравнение обеих схем функционального контроля по следующим показателям: сложности L; количеству входных наборов, на которых не обнаруживаются неисправности из заданного множества.
Таблица 3
|
Схема контроля |
Сложность L |
Количество входных наборов, на которых не обнаруживаются заданные неисправности |
|
дублирование |
80 |
0 |
|
паритет |
49 |
15 |
Отчет должен содержать
- функциональную схему КДУ с указанными на ней неисправностями;
- функции выходов f1, f2, f3, f4 исправного КДУ;
-
функции выходов ![]() для всех неисправностей;
для всех неисправностей;
- схемы функционального контроля методом дублирования и паритета;
- схему дополнительного блока паритета Р(х);
- таблицы 1, 2 и 3
Список литературы
1. Сапожников В.В., Сапожников Вл. В. Основы технической диагностики. М.; Маршрут, 2004.-318 c.
Приложение
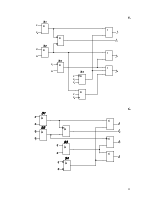
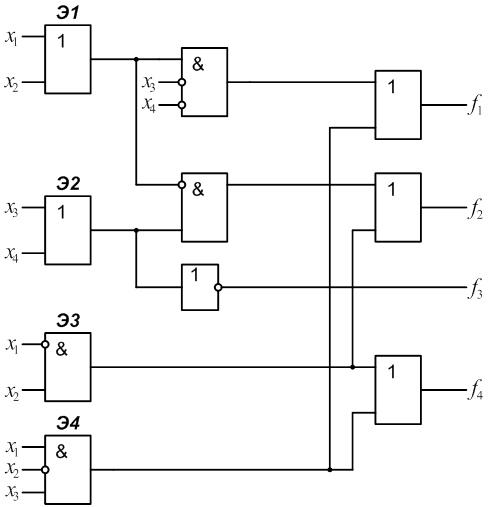
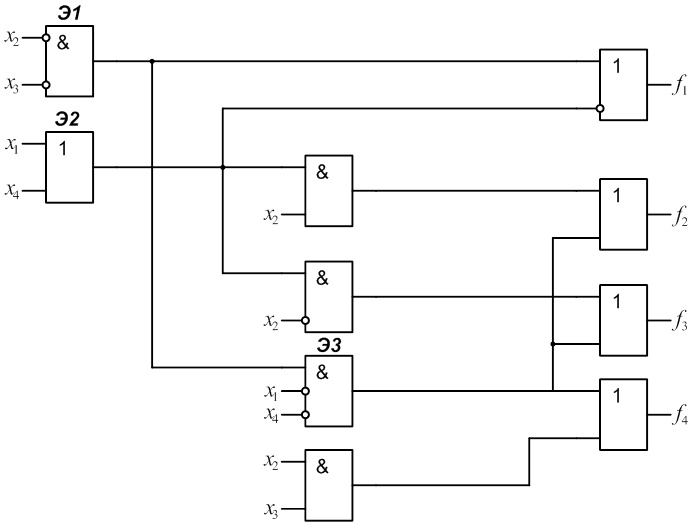
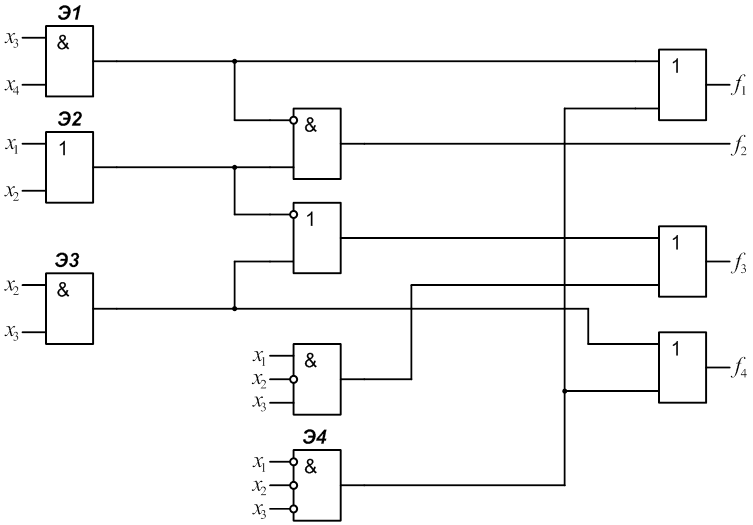
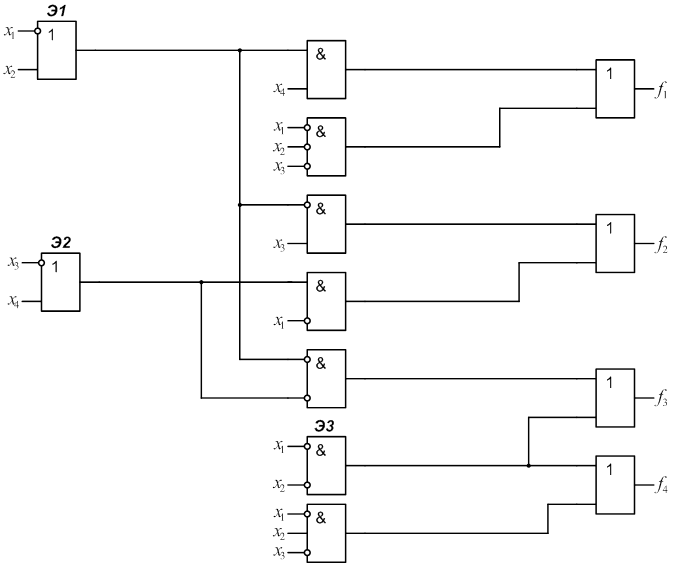
1.
2.
3.
4.
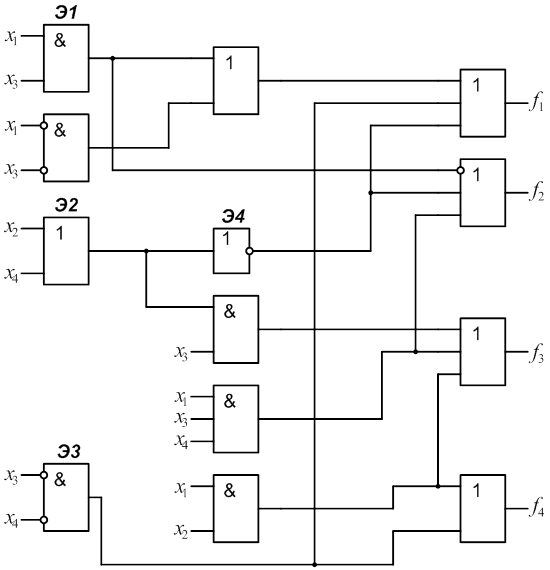
5.
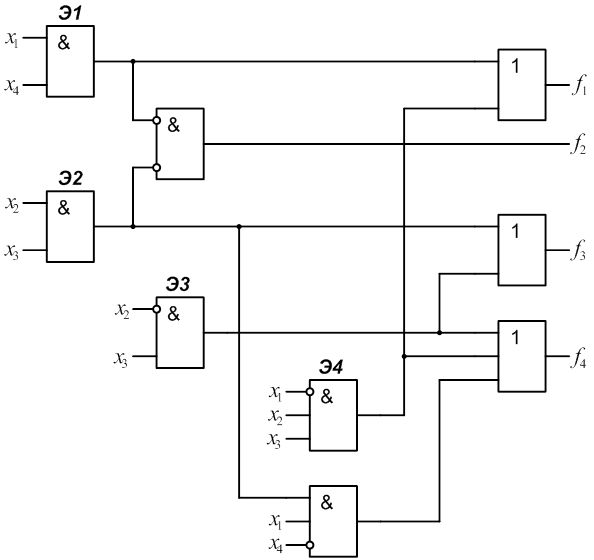
6.
7.
8.
9.
10.
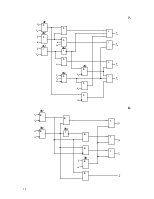
11.
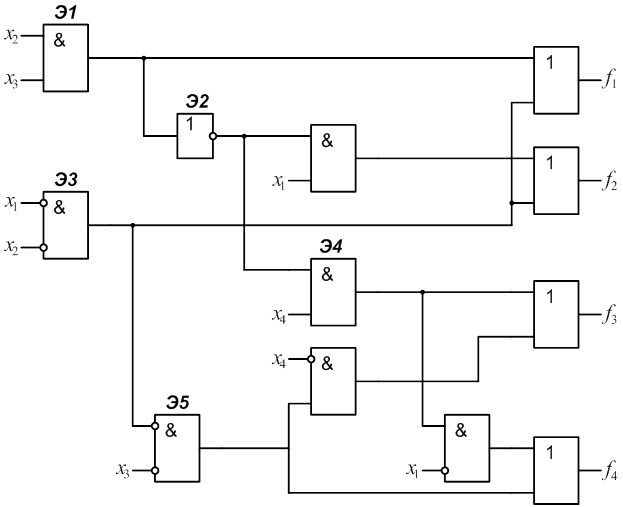
12.
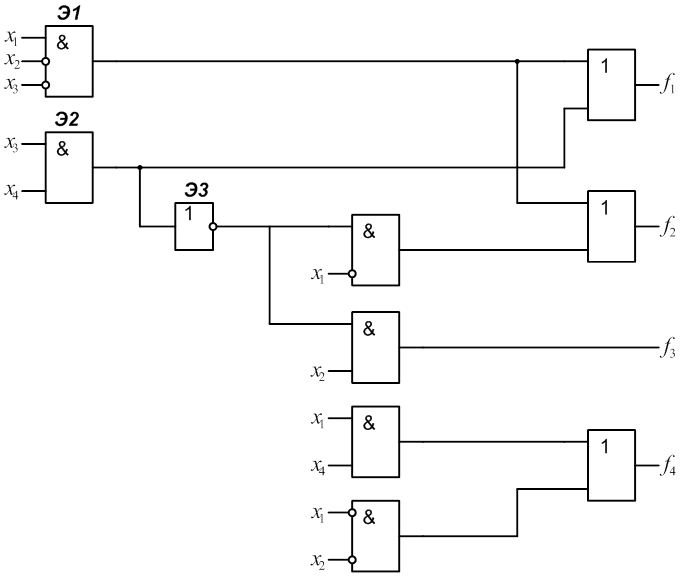
13.
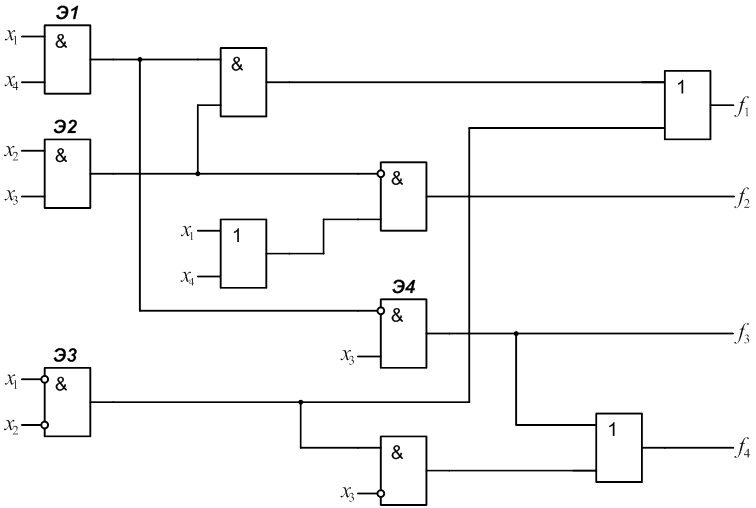
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.