Способ построения проекции угла. Перемена двух плоскостей проекций

Вопрос №35 Способ построения проекции угла между двумя плоскостями общего положения , заданных следами

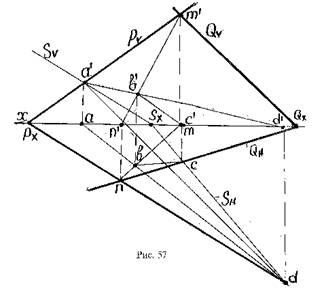
Пример. Заданы следы плоскостей Р и Q. Требуется определить проекции угла между плоскостями (рис. 57).

Решение: Определяется линия пересечения плоскостей Р и Q (линия MN, см. рис. 57). Строится вспомогательная плоскость S, перпендикулярная линии MN: точка S_X выбирается произвольно, след S_V проводится перпендикулярно линии m’n’, след S_H – перпендикулярно линии mn.

Определяется линия пересечения плоскостей Р и S (линия AD, см. рис. 57).

Находится точка пересечения линий KD и MN – точка В.

Определяется точка “С”, расположенная на линии пересечения плоскостей Q и S.

Точки b и c, b’ и c’ соединяются прямыми.

В результате построения получают две проекции угла АВС - Ðabc и Ða’b’c’.

Вопрос №36 В каких случаях применяется перемена двух плоскостей проекций. Привести пример.

 Сущность способа заключается в перемене одной или двух плоскостей проекций так, чтобы получить новое положение геометрического объекта, наиболее удобное для решения задачи.

В большинстве случаев бывает достаточно переменить только одну из старых плоскостей. Если этого недостаточно, то меняют две плоскости, причем последовательно, вначале заменяют одну плоскость, затем другую.

Способ перемены плоскостей проекций позволяет решать широкий круг задач, а именно: 1. Определять истинные размеры фигуры, истинные углы между линиями, между линией и плоскостью.

2. Определять расстояния от точки до линии, до плоскости, определять расстояние между прямыми и др. [3, 7]

Рассматриваются примеры замены двух плоскостей проекций.

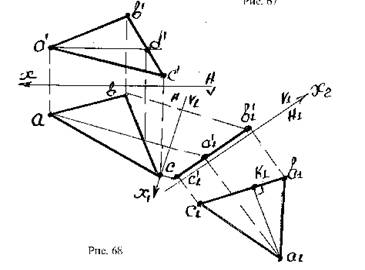
Пример 1. Заданы проекции треугольника АВС. Требуется определить площадь фигуры. (рис. 68)

Решение: Проводится горизонталь a’b’.

Выполняется перемена плоскости V: новая ось Х₁ располагается перпендикулярно линии ad (см. рис. 68).

Производится замена плоскости Н: ось Х₂ проводится параллельно линии b’₁c’₁ и строится новая горизонтальная проекция фигуры a₁b₁c₁. 

Поскольку эта фигура параллельна плоскости Н, следовательно она проектируется   на эту плоскость в свою натуральную величину.

Определяется площадь треугольника a₁b₁c₁: из точки a₁ опускается перпендикуляр на линию b₁c₁.

S_Δ-ки = ½· a₁ t₁ · b₁c₁