Диагностирование микропроцессорных систем, страница 8

          При структурном подходе тесты строятся с использованием информации о внутренней структуре программы. При этом применяют в основном три критерия (рис. 7.7):    1) проверку каждой команды не менее одного раза;          2) проверку каждой ветви программы не менее одного раза; 3) проверку каждого пути программы не менее одного раза. Последний критерий наиболее сильный. Если программа содержит циклы, то ограничиваются тестированием простых, ациклических путей или число итераций ограничивается некоторой константой.

          Рассматриваемая бинарная программа (см. рис. 7.8) содержит пять путей:  = 1, 10;  = 1, 2, 4, 5, 10;  = 1, 2, 4, 6, 9;  = 1, 2, 3, 7, 10;  = 1, 2, 3, 8, 9. Эти пути тестируются соответственно наборами следующего теста  = (000, 111, 110, 100, 101). Пусть, например, при написании программы (табл. 7.6) допущена ошибка: в команде № 18 вместо команды JZ (переход по нулевому результату) записана команда JNZ (переход по единичному результату). Эта ошибка обнаруживается набором входных данных 101. В правильной программе на данном наборе реализуется путь  = 1, 2, 3, 8, 9 и выходной результат f = 1. В программе с ошибкой реализуется путь  = 1, 2, 4, 5  и выходной результат  f = 0.

          Доказать полноту функционального или структурного теста в практических применениях сложно. Поэтому в общем случае тестирование не может доказать отсутствие ошибок в ПО, а может только обнаружить некоторую их часть.

7.4. Средства функционального диагностирования

микропроцессорных систем

          Области применения тестового диагностирования – производство, отладка и ремонт микропроцессорных систем. В процессе работы системы для обнаружения ошибок используются средства функционального контроля. В этом случае тестовыми воздействиями являются рабочие входные воздействия, а ошибки обнаруживаются практически немедленно. Однако, полнота контроля в целом меньше чем при тестировании. Эффективным является одновременное применение обоих видов контроля, когда периодически через некоторое время  выделяется интервал времени  для тестового диагностирования.

          В микропроцессорной системе выполняются три основные вида операций, которые надо контролировать: передача информации, логические и арифметические операции. Для их контроля используются аппаратные и программные методы (рис. 7.9).

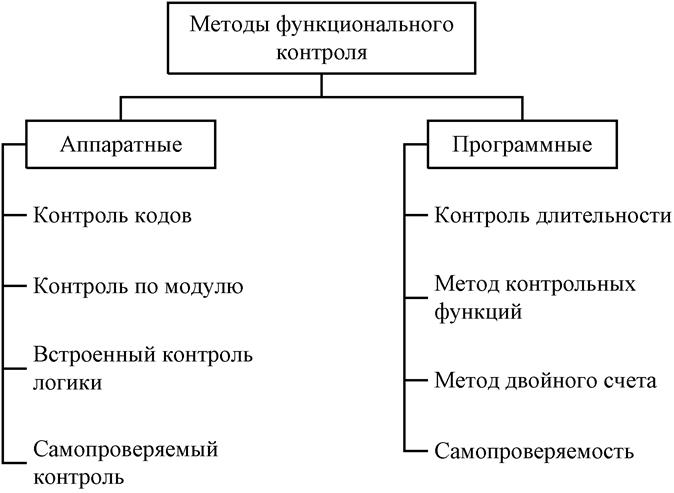
Рис.7.9. Методы функционального контроля микропроцессорных

                систем

 Аппаратный контроль  имеет высокое быстродействие, но требует дополнительных затрат аппаратуры. Программный контроль не связан с аппаратной избыточностью, но использует дополнительное процессорное время для выполнения программ контроля. В большинстве сложных микропроцессорных систем сочетаются аппаратные и программные средства контроля.

          При передаче информации для ее контроля используются избыточные коды с обнаружением и исправлением ошибок. Код называется избыточным, если для передачи информации используются не все возможные кодовые слова. В этом случае для n-разрядного кода выполняется неравенство , где N – число используемых кодовых слов (емкость кода). Кодовым расстоянием d называется минимальное число разрядов, которыми различаются два кодовых слова. Код с кодовым расстоянием d обнаруживает ошибки в t разрядах и менее, если выполняется неравенство

и исправляет ошибки в r разрядах и менее, если

.

          Коды с обнаружением ошибок применяются при передаче данных в шинах микропроцессорных систем и при хранении и передаче данных в регистрах. Наиболее часто используется для этих целей код с контролем на четность, который образуется добавлением одного избыточного (контрольного) разряда. Кодовое расстояние этого кода равно 2, что обеспечивает обнаружение всех одиночных ошибок и любого нечетного числа ошибок. Коды с исправлением ошибок используются в оперативной памяти, в запоминающих устройствах на магнитных лентах и дисках. Наиболее распространен код Хэмминга, который исправляет одиночные ошибки и обнаруживает двойные.

          Для контроля арифметических операций в цифровых ЭВМ широко используется контроль по модулю. В этом случае каждому числу А, участвующему в арифметической операции, сопоставляется остаток по модулю R, определяемый из равенства

,                                          (7.3)

где Q – модуль, а – целая часть отношения А/Q.

          Говорят, что числа  и  равны по модулю Q (), если их остатки равны ( = ). Для операций сложения, вычитания и умножения имеет место соотношение