Способ вращения. Способ перемены плоскостей, страница 2

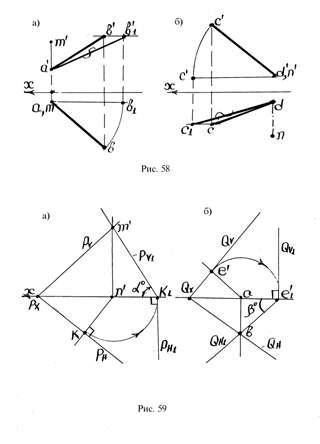
Пример 2. Заданы проекции точки А и следы плоскости Р. Требуется определить расстояние от точки А до плоскости Р (рис. 66).

Решение: Производится перемена плоскости Н: новая ось Х₁ проводится перпендикулярно следу Р_V.

Определяется новое положение горизонтального следа плоскости Р – Р_Н1.

Строится новая горизонтальная проекция точки А – а₁ (см. рис. 66).

Из точки а₁ опускается перпендикуляр на линию Р_Н1.

Поскольку плоскость Р преобразована в горизонтально-проектирующую плоскость, длина отрезка a₁k определяет расстояние от точки А до плоскости Р.

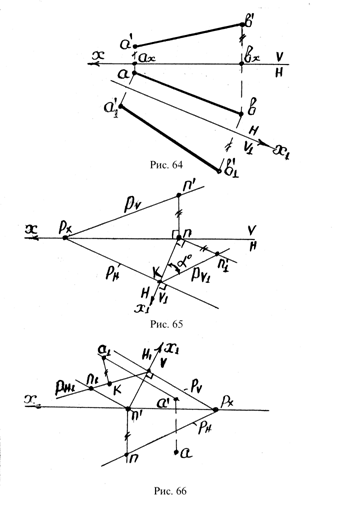
Рассматривается пример определения расстояния от точки а до плоскости треугольника BCD (рис. 67).

Решение: Через точку b проводится горизонталь b’k’.

Производится замена плоскости V на V₁: новая ось Х₁ проводится перпендикулярно линии bk.

Строятся новые фронтальные проекции точки А и треугольника BCD – a’₁ и b’₁c’₁d’₁.

Из точки a’₁ опускается перпендикуляр на линию b’₁c’₁.

Длина отрезка a’₁t’₁ определяет расстояние от точки А до плоскости фигуры BCD.

Из примеров, показанных на рис. 64, 65, 66, 67 видно, что для решения задачи достаточно было произвести замену одной плоскости проекции.