Трехмерное моделирование концепций качества, страница 4

Использование трехмерной формы для определения объема точности применимо к современной методике использования контрольных таблиц (графиков), которые применяют для уменьшения несоответствия (расхождения). Типичное применение контрольных таблиц - определение номинальной величины измеряемого признака, а затем применение соответствующего диапазона производственной ошибки, основываясь на допусках в спецификациях и исходя из верхнего и нижнего контрольных пределов. Цель уменьшить несоответствие и ограничить колебания в процессе достигается путем записи и анализа данных методом статистического управления процессом.

По мере того как конечный продукт становится все более сложным, большее значение придается способности всех подузлов и компонентов соответствовать друг другу и успешно функционировать вместе. Чтобы это было возможным, необходимо минимизировать совокупную (составную) ошибку критических признаков продукта (изделия), взятых как целое.

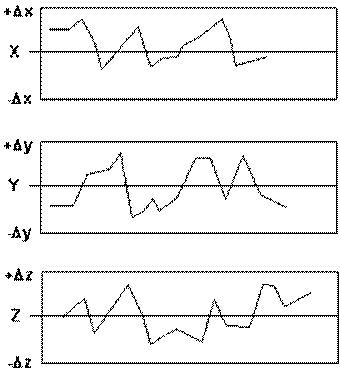
Рис. 7. Набор типичных контрольных таблиц для признаков x, y, z

Рис. 7 показывает типичный набор контрольных таблиц для признаков x, y, z. Эти признаки не обязательно должны быть единицами длины, это может быть любая группа из трех измеримых характеристик. Длина, вес, и напряжение, например. Для наших целей, однако, используется простая модель с идентичной допустимой ошибкой. Как показано на рис. 7, когда каждый признак измеряется и показывается на таблице, признак остается в пределах допусков. Цель трехмерной модели - уменьшить колебание совокупной ошибки, что может повлиять на работу или функцию компонента.

Трехмерная форма (в нашем случае куб) определяется путем установления определенных значений вдоль осей x, y, z (рис.8). Этот объем точности ограничивается допустимой ошибкой для каждого признака (± D x, ± D y, ± D z) и центр его расположен в точке, определенной точными спецификациями в (x, y, z). Поскольку данные собираются и наносятся для каждого из трех признаков и пока x, y, z остаются в рамках установленных пределов, ожидается, что трехмерная точка x, y, z окажется внутри границ объема, очерченного кубом.

Рис. 8. Объем точности, определяемый кубом

Однако, точность может быть повышена, колебание может быть увеличено и совокупная ошибка может быть минимизирована, если определить объем точности как сферу, диаметр которой расположен в той же точке, которая определена спецификациями, данными на рис. 9. В этом случае, используя идентичные допуски (или нормализованные допуски, когда используются различные единицы измерения), может быть получена сфера с радиусом r, где r=D x²+D y²+D z². В отличии от куба, границы сферы равноудалены от центральной точки и совокупная ошибка лучше контролируется. Используя границы сферы вместо куба как Объем точности, точка данных , определяемая когда признак находится на контрольном пределе (границе) или вблизи от него, больше не является удовлетворительной. В смысле объема, сфера центр которой находится в той же точке, что и центр куба, занимает только половину объема, занимаемого кубом.

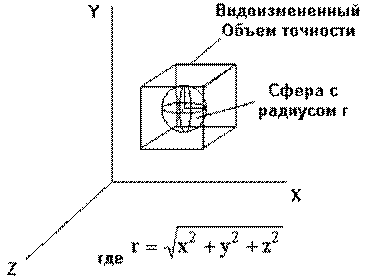
Рис. 9. Объем точности, определяемый сферой с радиусом r

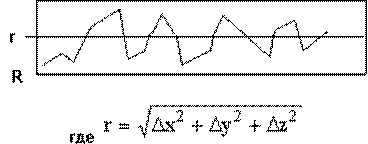
Рис. 10. Радиус r, вычисленный и нанесенный на контрольный график

Рис. 10 показывает, как это может быть представлено на стандартном контрольном графике, используя простые расчеты с радиусом сферического Объема точности, ограниченного 0 и r, где r - максимальная допустимая совокупная ошибка.

Выводы .

Представлены только 3 возможных применения трехмерного моделирования. Эти модели относительно просты и могут помочь не только объяснить некоторые из концепций, но также могут использоваться для уменьшения несоответствия в производстве.