Типовой расчет по высшей математике «Элементы математической статистики»

Министерство образования РФ

Ульяновский государственный технический университет

Институт авиационных технологий и управления

Кафедра общенаучных дисциплин

ТИПОВОЙ РАСЧЕТ ПО ВЫСШЕЙ МАТЕМАТИКЕ

«ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ»

Вариант №26

Выполнил:

Студент группы

 АСВд-21

Чирков М.А.

Проверила:

Карасёва А.Г.

 Ульяновск 2006 год.

Задание:

7,55	7,40	7,26	7,42	7,50	7,43	7,51	7,43	7,60	7,44
7,63	7,38	7,44	7,52	7,53	7,44	7,31	7,58	7,28	7,24
7,53	7,39	7,57	7,51	7,34	7,43	7,37	7,29	7,54	7,33
7,58	7,57	7,33	7,51	7,40	7,27	7,52	7,40	7,26	7,66
7,40	7,52	7,56	7,40	7,34	7,41	7,34	7,43	7,38	7,50
7,35	7,36	7,40	7,45	7,29	7,41	7,38	7,14	7,42	7,52
7,59	7,47	7,62	7,54	7,20	7,30	7,54	7,38	7,37	7,34
7,47	7,40	7,29	7,20	7,46	7,40	7,57	7,31	7,40	7,36
7,39	7,50	7,38	7,45	7,50	7,37	7,28	7,39	7,32	7,20
7,55	7,33	7,32	7,69	7,46	7,33	7,45	7,31	7,45	7,39

1.  Определить частоты n_i, относительную частоту _i, составить статистический ряд.

2.  Определить выборочную среднюю, выборочную дисперсию, среднее квадратичное отклонение.

3.  Построить график распределения.

4.  Простроить в одной системе координат гистограмму и теоретическую функцию плотности распределения вероятности.

5.  Вычислить выравнивающие частоты n_i⁰.

6.  Пользуясь критерием Пирсона проверить согласованность гипотезы о нормальном распределении с уровнем надежности α =0,05.

7.   Построить доверительный интервал припри известном σ.

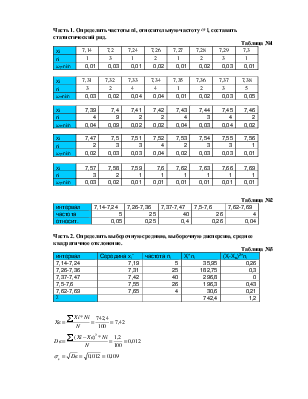
Часть 1. Определить частоты ni, относительную частоту i, составить статистический ряд.

Таблица №1

Хi	7,14	7,2	7,24	7,26	7,27	7,28	7,29	7,3
ni	1	3	1	2	1	2	3	1
ωi=ni/n	0,01	0,03	0,01	0,02	0,01	0,02	0,03	0,01
								J
Хi	7,31	7,32	7,33	7,34	7,35	7,36	7,37	7,38
ni	3	2	4	4	1	2	3	5
ω=ni/n	0,03	0,02	0,04	0,04	0,01	0,02	0,03	0,05
Хi	7,39	7,4	7,41	7,42	7,43	7,44	7,45	7,46
ni	4	9	2	2	4	3	4	2
ωi=ni/n	0,04	0,09	0,02	0,02	0,04	0,03	0,04	0,02
Хi	7,47	7,5	7,51	7,52	7,53	7,54	7,55	7,56
ni	2	3	3	4	2	3	3	1
ωi=ni/n	0,02	0,03	0,03	0,04	0,02	0,03	0,03	0,01
Хi	7,57	7,58	7,59	7,6	7,62	7,63	7,66	7,69
ni	3	2	1	1	1	1	1	1
ωi=ni/n	0,03	0,02	0,01	0,01	0,01	0,01	0,01	0,01

Таблица №2

интервал	7,14-7,24	7,26-7,36	7,37-7,47	7,5-7,6	7,62-7,69
частота	5	25	40	26	4
относит.	0,05	0,25	0,4	0,26	0,04

Часть 2. Определить выборочную среднюю, выборочную дисперсию, среднее квадратичное отклонение.

Таблица №3

интервал	Середина xi~	частота ni	Xi*ni	(Xi-Xв)2*ni
7,14-7,24	7,19	5	35,95	0,26
7,26-7,36	7,31	25	182,75	0,3
7,37-7,47	7,42	40	296,8	0
7,5-7,6	7,55	26	196,3	0,43
7,62-7,69	7,65	4	30,6	0,21
∑			742,4	1,2

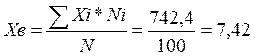
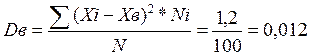
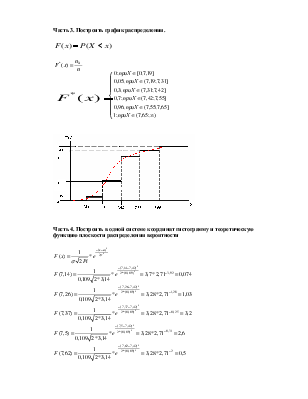
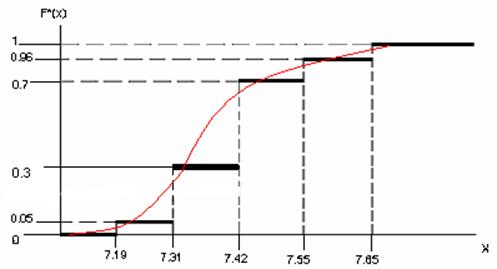
Часть 3. Построить график распределения.

 

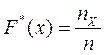
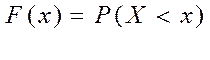
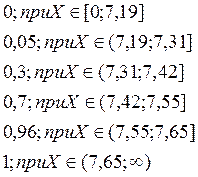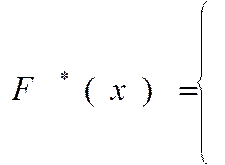
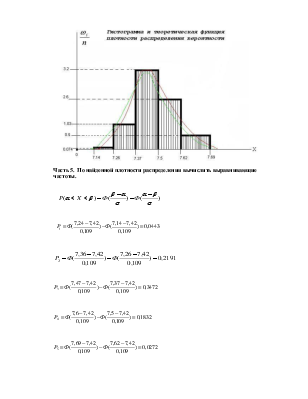
Часть 4. Построить в одной системе координат гистограмму и теоретическую функцию плоскости распределения вероятности

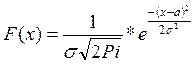
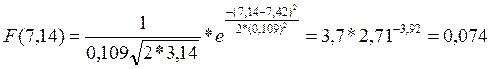
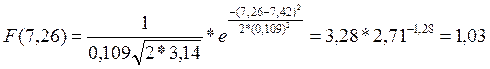
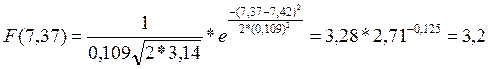
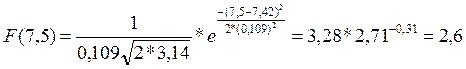
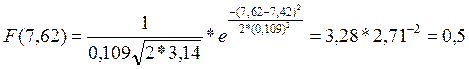
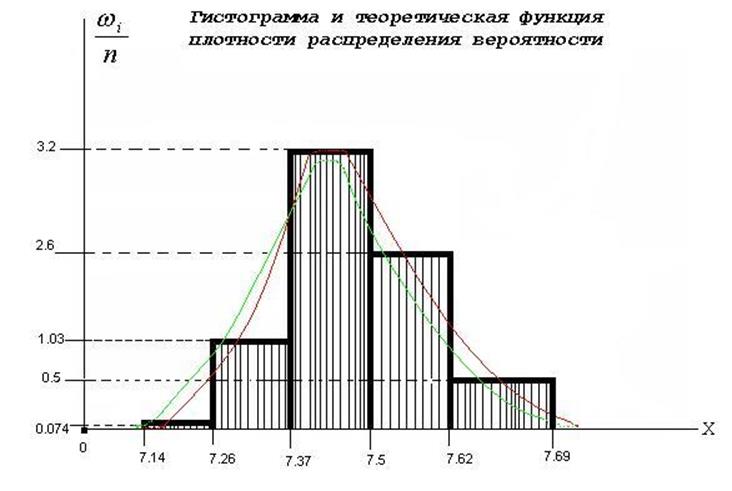
Часть 5.  По найденной плотности распределения вычислить выравнивающие частоты.

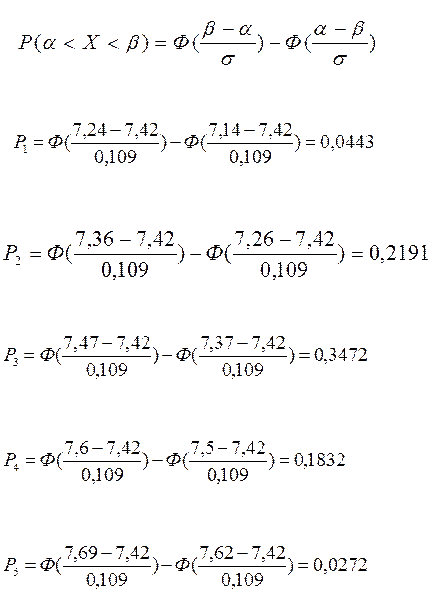
n_i⁰=P_i*n

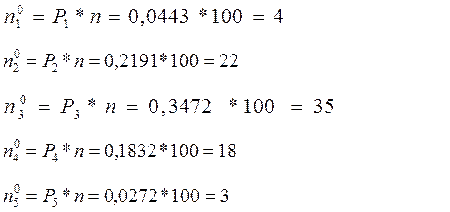
Часть 6. Пользуясь критерием Пирсона проверить согласованность гипотезы о нормальном распределении с уровнем надежности α =0,05.

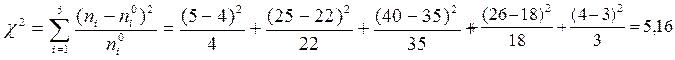
S=K-1-2=5-3=2

α=0,05

K = Xmax-Xmin/0,1

K = 7,69-7,14/0,1=5,4

Гипотеза о нормальном распределении принимается т.к она согласуется с экспериментальными данными.

Часть 7. Построить доверительный интервал припри известном σ.

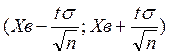
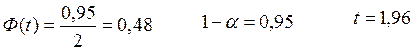
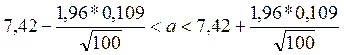
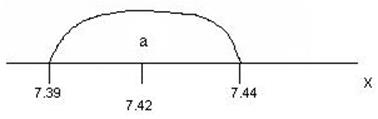
Р=(7,39<а<7,44)=0,95