Абсолютное значение одного процента прироста (А1%) : как одна сотая часть предыдущего уровня.
Полученные в результате вычислений значения внесем в таблицу №5 «Основные показатели ряда динамики».
Таблица №5 «Основные показатели ряда динамики»
|
Показатели |
2000 |
2001 |
2002 |
2003 |
2004 |
|
Сумма доходов в месяц на семью, руб., х |
860 |
1110 |
950 |
980 |
940 |
|
Абсолютное отклонение, |
|||||
|
- цепное |
=C2-B2 |
=D2-C2 |
=E2-D2 |
=F2-E2 |
|
|
- базисное |
=C2-B2 |
=D2-B2 |
=E2-B2 |
=F2-B2 |
|
|
Коэффициент роста |
|||||
|
- цепной |
=C2/B2 |
=D2/C2 |
=E2/D2 |
=F2/E2 |
|
|
- базисный |
=C2/B2 |
=D2/B2 |
=E2/B2 |
=F2/B2 |
|
|
Темп роста, % |
|||||
|
- цепной |
=C2/B2*100 |
=D2/C2*100 |
=E2/D2*100 |
=F2/E2*100 |
|
|
- базисный |
100 |
=C2/B2*100 |
=D2/B2*100 |
=E2/B2*100 |
=F2/B2*100 |
|
Темп прироста, % |
|||||
|
- цепной |
=C10-100 |
=D10-100 |
=E10-100 |
=F10-100 |
|
|
- базисный |
=C11-100 |
=D11-100 |
=E11-100 |
=F11-100 |
|
|
Абсолютное значение 1процента прироста |
|||||
|
- цепное |
=B2/100 |
=C2/100 |
=D2/100 |
=E2/100 |
|
|
- базисное |
Таблица № 5 «Основные показатели ряда динамики»
|
Показатели |
2000 |
2001 |
2002 |
2003 |
2004 |
|
Сумма доходов в месяц на семью, руб., х |
860 |
1110 |
950 |
980 |
940 |
|
Абсолютное отклонение, |
|||||
|
- цепное |
250 |
-160 |
30 |
-40 |
|
|
- базисное |
250 |
90 |
120 |
80 |
|
|
Коэффициент роста |
|||||
|
- цепной |
1,29 |
0,86 |
1,03 |
0,96 |
|
|
- базисный |
1,29 |
1,10 |
1,14 |
1,09 |
|
|
Темп роста, % |
|||||
|
- цепной |
129,07 |
85,59 |
103,16 |
95,92 |
|
|
- базисный |
100 |
129,07 |
110,47 |
113,95 |
109,30 |
|
Темп прироста, % |
|||||
|
- цепной |
29,07 |
-14,41 |
3,16 |
-4,08 |
|
|
- базисный |
29,07 |
10,47 |
13,95 |
9,30 |
|
|
Абсолютное значение 1процента прироста |
|||||
|
- цепное |
8,6 |
11,1 |
9,5 |
9,8 |
|
|
- базисное |
Рассчитаем среднегодовые значения этих показателей:
Средний уровень (![]() ) исчисляется по формуле средней
арифметической простой:
) исчисляется по формуле средней
арифметической простой:
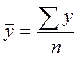 =
(860+1110+950+980+940) : 5 = 4840 : 5 = 968
=
(860+1110+950+980+940) : 5 = 4840 : 5 = 968
где у – уровни ряда.
Средний абсолютный прирост исчисляется как средняя арифметическая простая годовых (цепных) приростов:
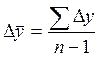 = (29,07 + (-14,41) + 3,16 + (-4,08)) : 4 =
13,73 : 4 = 3,43
= (29,07 + (-14,41) + 3,16 + (-4,08)) : 4 =
13,73 : 4 = 3,43
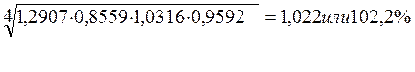 Среднегодовой темп роста исчисляется по формуле
средней геометрической из цепных коэффициентов роста:
Среднегодовой темп роста исчисляется по формуле
средней геометрической из цепных коэффициентов роста:
![]() =
=
где n – число коэффициентов;
![]() - знак произведения.
- знак произведения.
Среднегодовой темп
прироста исчисляется следующим образом: ![]() или
или ![]()
![]() = 102,2 - 100 = 2,2 %
= 102,2 - 100 = 2,2 %
![]() = 1,022 - 1,0 = 0,022
= 1,022 - 1,0 = 0,022
Расчет среднего абсолютного значения одного процента прироста за несколько лет производится по формуле:
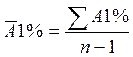 = (8,6 + 11,1 + 9,5 + 9,8) : 4 = 39 : 4 =
9,75
= (8,6 + 11,1 + 9,5 + 9,8) : 4 = 39 : 4 =
9,75
Вывод: В результате выполненных расчетов я определила размер среднего абсолютного значения одного процента прироста за несколько лет он равен 9,75%
Задача №4
Условие:
По данным о реализации товаров (по шести видам товаров) (приложение 3) определить:
- индивидуальные индексы (ip, iq);
- сводные индексы (Ip, Iq, Ipq);
- абсолютное изменение товарооборота за счет:
1) количества товаров;
2) изменения цен;
Сделать вывод по решению задачи.
Решение:
|
Приложение №3 |
||||
|
Вид продукции |
Базисный период |
Отчетный период |
||
|
количеств, |
цена, |
количество, |
цена, |
|
|
q0 |
p0 |
q1 |
p1 |
|
|
E |
170 |
110 |
180 |
110 |
|
R |
3320 |
30 |
3160 |
31 |
|
T |
430 |
205 |
470 |
204 |
|
Y |
570 |
10 |
540 |
11 |
|
U |
610 |
43 |
630 |
47 |
|
I |
33 |
502 |
29 |
501 |
На основании приложения №3 заполним таблицу №4, затем по формулам представленным ниже рассчитаем требуемые по условию задачи показатели и внесем их в таблицу №6. По полученным в результате вычислений данным сделаем вывод.
|
Таблица № 6 |
|||||||||
|
Вид |
Базисный период |
Отчетный период |
Произведение |
Индивидуальные индексы |
|||||
|
кол-во, |
цена, |
кол-во, |
цена, |
q0*p0 |
q1*p0 |
q1*p1 |
q1/q0 |
p1/p0 |
|
|
q0 |
p0 |
q1 |
p1 |
||||||
|
1 |
170 |
110 |
180 |
110 |
18700 |
19800 |
19800 |
1,06 |
1,00 |
|
2 |
3320 |
30 |
3160 |
31 |
99600 |
94800 |
97960 |
0,95 |
1,03 |
|
3 |
430 |
205 |
470 |
204 |
88150 |
96350 |
95880 |
1,09 |
1,00 |
|
4 |
570 |
10 |
540 |
11 |
5700 |
5400 |
5940 |
0,95 |
1,10 |
|
5 |
610 |
43 |
630 |
47 |
26230 |
27090 |
29610 |
1,03 |
1,09 |
|
6 |
33 |
502 |
29 |
501 |
16566 |
14558 |
14529 |
0,88 |
1,00 |
|
Итого |
- |
- |
- |
- |
254946 |
257998 |
263719 |
- |
- |
![]() = 257998 - 254946 =
3052
= 257998 - 254946 =
3052
![]() = 263719 - 257998 =
5721
= 263719 - 257998 =
5721
![]() = 5721 + 3052 = 8773
= 5721 + 3052 = 8773
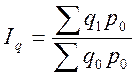 = 257998 : 254946 =
1,01
= 257998 : 254946 =
1,01
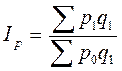 = 263719 : 257998 =
1,02
= 263719 : 257998 =
1,02
Ipq = Ip * Iq= 1,02 * 1,01 = 1,03
Вывод: В результате расчетов я выяснила индивидуальный индекс физического объема продукции , который показал что произошло увеличение объёмов реализованной продукции в отчетном периоде по сравнению с базисным на 0,88 -1,09 раз. Рассчитав индивидуальные индекс цен я увидела что прибыль за счет увеличения цены на продукцию в отчетном периоде выросла по сравнению с базисным и составила 1,01 %. В итоге можно сказать, что увеличение размера прибыли на 1,02 % произошло главным образом за счет увеличения цены.
Задача №4
Условие:
Из исходных данных таблицы 1 (выбрать строки с 14 по 23) провести корреляционно-регрессионный анализ, определить параметры корреляции и детерминации. Построить график корреляционной зависимости между двумя признаками (результативным и факторным). Сделать вывод.
Решение:
|
Таблица №7 "Исходные данные" |
||
|
Порядковый номер рабочего |
Производственный стаж (лет) |
Размер заработной платы (д.е.) |
|
14 |
20 |
1800 |
|
15 |
40 |
2800 |
|
16 |
14 |
1750 |
|
17 |
9 |
1580 |
|
18 |
14 |
1750 |
|
19 |
20 |
1560 |
|
20 |
9 |
1210 |
|
21 |
10 |
1200 |
|
22 |
6 |
1355 |
|
23 |
12 |
1480 |
На основании данных таблицы №7 «Исходные данные» заполним таблицу № 8:
|
Таблица №8 |
|||||
|
№п/п |
х |
у |
х*у |
х2 |
y2 |
|
1 |
10 |
1200 |
12000 |
100 |
1440000 |
|
2 |
9 |
1210 |
10890 |
81 |
1464100 |
|
3 |
6 |
1355 |
8130 |
36 |
1836025 |
|
4 |
12 |
1480 |
17760 |
144 |
2190400 |
|
5 |
20 |
1560 |
31200 |
400 |
2433600 |
|
6 |
9 |
1580 |
14220 |
81 |
2496400 |
|
7 |
14 |
1750 |
24500 |
196 |
3062500 |
|
8 |
14 |
1750 |
24500 |
196 |
3062500 |
|
9 |
20 |
1800 |
36000 |
400 |
3240000 |
|
10 |
40 |
2800 |
112000 |
1600 |
7840000 |
|
Итого |
154 |
16485 |
291200 |
3234 |
29 065 525,00 |
Проведем корреляционно-регрессионный анализ и определим параметры корреляции и детерминации. Корреляционный и регрессивный анализ как общее понятие включает в себя измерение тесноты, направления связи и установления аналитического выражения (формы) связи (регрессивный анализ). В нашем случае нам предлагается линейная форма регрессии, уравнение прямой будет иметь вид:
![]()
где![]() - теоретические уровни;
- теоретические уровни;
а0 и а1 – параметры прямой.
Для нахождения параметров а0 и а1 необходимо решить систему нормальных уравнений:
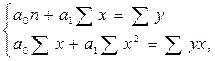
где у – фактические уровни ряда динамики;
n – число уровней.
Для решения системы используем метод определителей.
Параметры рассчитывают по формулам:
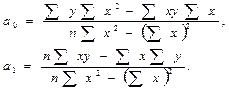
Итак, рассчитаем параметры:
a0 = (16485*3234)-(291200*154) : 10*3234-23716= 981,875
a1 = (10*291200) - (154*16485) : 10*3234 - 23716 = 43,287
Решим систему нормальных уравнений подставив вычисленные раннее параметры:
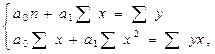
981,875 * 10 + 43,287 * 154 = 16485
981,875 * 154 + 43,287 * 3234 = 291200,
16485 = 16485
291200 = 291200
Подставим вычисленные параметры в уравнение прямой:
![]()
Рассчитаем коэффициент корреляции по формуле:
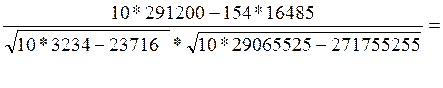
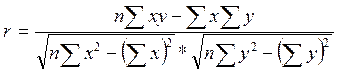 =
=
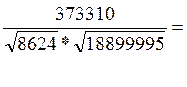 |
= 373310 : (92,86 * 4347,41) = 373310 : 403700,5 = 0,92
Коэффициент детерминации равен:
r2 = 0,92 * 092 = 0,85
Построим график корреляционной зависимости между двумя признаками (результативным и факторным), отложив на оси Х в порядке возрастания показатели стажа работы, на оси Y — данные по заработной плате:
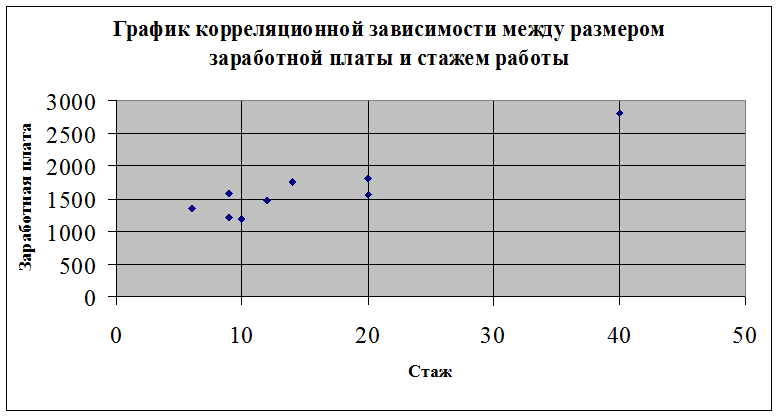
Вывод: График данного корреляционного поля позволяет предположить, что, возможно, между стажем работы и размером заработной платы у исследуемой группы наблюдается прямая, зависимость, т.е. со снижением показателя стажа работы происходит уменьшение размера заработной
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.